【题目】已知定义在![]() 上的函数
上的函数![]() 的图像经过点
的图像经过点![]() ,且
,且![]() 在区间
在区间![]() 单调递减,又知函数
单调递减,又知函数![]() 为偶函数,则关于
为偶函数,则关于![]() 的不等式
的不等式![]() 的解为 ( )
的解为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】本题用排除法比较简单,因为函数![]() 的图象经过点
的图象经过点![]() ,所以
,所以![]() 错误,
错误, ![]() 不合题意, 可排除选项A;又因为
不合题意, 可排除选项A;又因为![]() 在区间
在区间![]() 单调递减,所以
单调递减,所以![]() ,即
,即![]() 错误,
错误, ![]() 不合题意;可排除选项C、D,故选B.
不合题意;可排除选项C、D,故选B.
【 方法点睛】本题主要考查函数的奇偶性、单调性、排除法解选择题,属于难题.排除法解答选择题是高中数学一种常见的解题思路和方法,这种方法即可以提高做题速度和效率,又能提高准确性,这种方法主要适合下列题型:(1)求值问题(可将选项逐个验证);(2)求范围问题(可在选项中取特殊值,逐一排除);(3)图象问题(可以用函数性质及特殊点排除);(4)解方程、求解析式、求通项、求前![]() 项和公式问题等等.
项和公式问题等等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
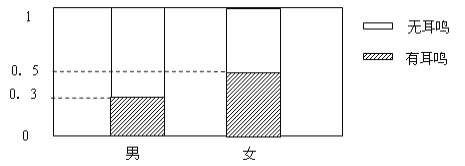
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
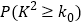
0.025
0.010
0.005
0.001
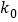
5.024
6.635
7.879
10.828
附:
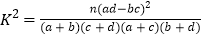
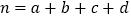
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生

表2:女生

(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
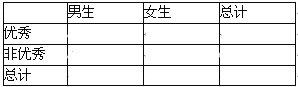
参考数据与公式:
K2=
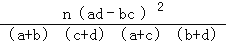 ,其中n=a+b+c+d.
,其中n=a+b+c+d.临界值表:

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2x+
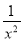 (x∈R).
(x∈R).(1)当x∈(0,1]时,求f(x)的解析式.
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
-
科目: 来源: 题型:
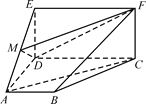
查看答案和解析>>【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,
 ,M是线段AE上的动点.
,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
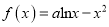 .
.(1)当
 时,求函数
时,求函数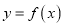 在
在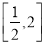 上的最大值;
上的最大值;(2)令
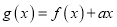 ,若
,若 在区间
在区间 上为单调递增函数,求
上为单调递增函数,求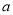 的取值范围;
的取值范围;(3)当
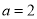 时,函数
时,函数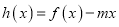 的图象与
的图象与 轴交于两点
轴交于两点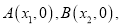 且
且 ,又
,又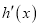 是
是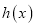 的导函数.若正常数
的导函数.若正常数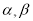 满足条件
满足条件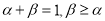 .证明:
.证明: 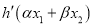 <0.
<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份
2008
2009
2010
2011
2012
2013
2014
年份代号t
1
2
3
4
5
6
7
人均纯收入y
2.7
3.6
3.3
4.6
5.4
5.7
6.2
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
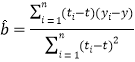 ,
,
相关试题

