【题目】2012年,商品价格一度成为社会热点话题,某种新产品投放市场的100天中,前40天价格呈直线上升,由于政府及时采取有效措施,从而使后60天的价格呈直线下降,现统计出其中4天的价格如下表
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(元) | 23 | 30 | 22 | 7 |
(1)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天);
(2)销售量g(x)与时间x的函数关系: ![]() (1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元?
(1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元?
参考答案:
【答案】
(1)解:由题意知,当1≤x<40时,一次函数y=ax+b过点A(4,23),B(32,30),代入函数求得a= ![]() ,b=22;
,b=22;
当40≤x≤100时,一次函数y=kx+m过点C(60,22),D(90,7),代入函数求得k=﹣ ![]() ,m=52;
,m=52;
∴函数解析式为:y=f(x)= 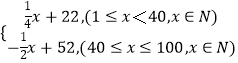
(2)解:设日销售额为S千元,当1≤x<40时,S(x)=( ![]() x+22)(﹣
x+22)(﹣ ![]() x+
x+ ![]() )=﹣
)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ;
;
∴当x=10或11时,函数有最大值S(x)max= ![]() =808.5(千元);
=808.5(千元);
当40≤x≤100时,S(x)=(﹣ ![]() x+52)(﹣
x+52)(﹣ ![]() x+
x+ ![]() )=
)= ![]() (x2﹣213x+11336);
(x2﹣213x+11336);
∴当x=40时,s(x)max=736(千元).
综上所知,日销售额最高是在第10天或第11天,最高值为808.5千元
【解析】(1)价格直线上升,直线下降,说明价格函数f(x)是一次函数,由表中对应关系用待定系数法易求f(x)的表达式;(2)由销售额=销售量×时间,得日销售额函数S(x)的解析式,从而求出S(x)的最大值.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)为定义R在的偶函数,当0≤x≤2时,y=
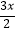 ;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
(1)求函数f(x)的解析式;
(2)在下面的直角坐标系中直接画出函数f(x)的图象,写出函数f(x)的单调区间(无需证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  ,
,  ,且
,且 的最小值为
的最小值为 .
.(1)求
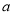 的值;
的值;(2)若不等式
 对任意
对任意 恒成立,其中
恒成立,其中 是自然对数的底数,求
是自然对数的底数,求 的取值范围;
的取值范围;(3)设曲线
 与曲线
与曲线 交于点
交于点 ,且两曲线在点
,且两曲线在点 处的切线分别为
处的切线分别为 ,
,  .试判断
.试判断 ,
,  与
与 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得aman=16a12 , 则
 +
+  的最小值为( )
的最小值为( )
A.
B.
C.
D.不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=
 ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A.AC⊥BF
B.直线AE,BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角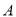 ,
, 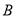 ,
, 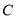 的对边分别为
的对边分别为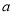 ,
, 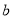 ,
, 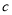 .已知
.已知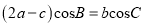 .
.(1)求角
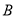 的大小;
的大小;(2)若
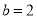 ,
, 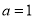 ,求
,求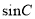 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2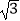 ﹣4,﹣2
﹣4,﹣2 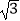 ?+4]
?+4]
B.(﹣∞,﹣2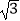 ﹣4]∪[﹣2
﹣4]∪[﹣2 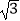 ?+4,+∞)
?+4,+∞)
C.[﹣2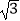 ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ]
]
相关试题

