【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
参考答案:
【答案】D
【解析】解:若f(x)≥mx对任意的实数x≥2都成立, 则m≤x+ ![]() ﹣4对任意的实数x≥2都成立,
﹣4对任意的实数x≥2都成立,
由对勾函数的图像和性质,可得
y=x+ ![]() ,(x≥2)在x=2时,取最小值
,(x≥2)在x=2时,取最小值 ![]() ,
,
故m≤ ![]() ﹣4=﹣
﹣4=﹣ ![]() ,
,
即实数m的取值范围是(﹣∞,﹣ ![]() ],
],
故选:D
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年,商品价格一度成为社会热点话题,某种新产品投放市场的100天中,前40天价格呈直线上升,由于政府及时采取有效措施,从而使后60天的价格呈直线下降,现统计出其中4天的价格如下表
时间
第4天
第32天
第60天
第90天
价格(元)
23
30
22
7
(1)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天);
(2)销售量g(x)与时间x的函数关系: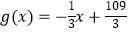 (1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元?
(1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=
 ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A.AC⊥BF
B.直线AE,BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角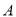 ,
, 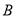 ,
, 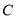 的对边分别为
的对边分别为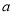 ,
, 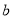 ,
, 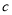 .已知
.已知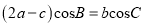 .
.(1)求角
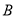 的大小;
的大小;(2)若
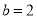 ,
, 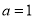 ,求
,求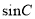 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 中,
中, 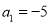 ,
,  ,
,  .数列
.数列 的前n项和为
的前n项和为 ,满足
,满足 ,
,  .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;(3)若数列
 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设 ,则当
,则当 ,
, 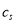 ,
,  和
和 ,
,  ,
,  均成等差数列时,求正整数
均成等差数列时,求正整数 ,
,  ,
,  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=logax,g(x)=loga(2x+t﹣2)2 , (a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2]时F(x)=g(x)﹣f(x)有最小值为2,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
(备注:函数y=x+ 在区间(0,1)上单调递减,在区间(1,+∞)上单调递增).
在区间(0,1)上单调递减,在区间(1,+∞)上单调递增). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为 , 表面积为 .
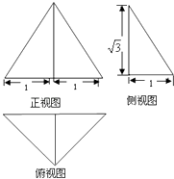
相关试题

