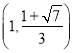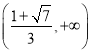【题目】已知函数![]() ,
, ![]() ,
, ![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .试判断
.试判断![]() ,
, ![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
参考答案:
【答案】(1)![]() .(2)
.(2)![]() . (3)
. (3)![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.
【解析】试题分析:
(1)由原函数与导函数的关系可求得a=-2;
(2) 不等式即![]() ,构造函数令
,构造函数令![]() ,分类讨论可得
,分类讨论可得![]() 的取值范围是
的取值范围是![]() .
.
(3) 设![]() ,
, ![]() 的倾斜角分别为
的倾斜角分别为![]() ,
, ![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴所围成的三角形是等腰三角形,则
轴所围成的三角形是等腰三角形,则![]() 或
或![]() . 分类讨论:
. 分类讨论: ![]() 和
和![]() 两种情况可得
两种情况可得![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.
试题解析:
(1)![]() ,所以
,所以![]() ,则
,则![]() 的最小值为
的最小值为![]() ,
,
因此抛物线![]() 的对称轴为
的对称轴为![]() ,即
,即![]() ,所以
,所以![]() .
.
(2)由(1)知, ![]() .不等式
.不等式![]() 即
即![]() ,
,
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
①若![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调减,
上单调减,
故![]() ,解得
,解得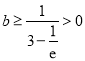 ,
,
此时无符合题意的![]() 值; ②若
值; ②若![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
由题意,可知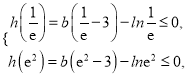 解得
解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() ,
, ![]() 的倾斜角分别为
的倾斜角分别为![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,
, ![]() ,则
,则![]() ,
, ![]() 均为锐角.
均为锐角.
若![]() ,
, ![]() 与
与![]() 轴所围成的三角形是等腰三角形,则
轴所围成的三角形是等腰三角形,则![]() 或
或![]() .
.
①当![]() 时,
时, ![]() ,即
,即![]() ,解得
,解得![]() ,
,
而![]() ,即
,即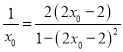 ,
,
整理得, ![]() ,解得
,解得![]() .
.
所以存在唯一的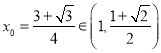 满足题意.
满足题意.
②当![]() 时,由
时,由![]() 可得
可得![]() ,
,
而![]() ,即
,即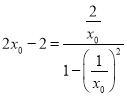 ,
,
整理得, ![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() .列表如下:
.列表如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
而![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 在
在![]() 内有一个零点,也是
内有一个零点,也是![]() 上的唯一零点.
上的唯一零点.
所以存在唯一的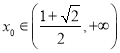 满足题意.
满足题意.
综上所述, ![]() ,
, ![]() 与
与![]() 轴能围成2个等腰三角形.
轴能围成2个等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1点E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成的角是( )
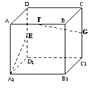
A.90°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】四面体的六条棱中,有五条棱长都等于a,则该四面体的体积的最大值为( )
A. ?a3
?a3
B. ?a3
?a3
C. ?a3
?a3
D.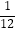 ?a3
?a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)为定义R在的偶函数,当0≤x≤2时,y=
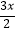 ;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
(1)求函数f(x)的解析式;
(2)在下面的直角坐标系中直接画出函数f(x)的图象,写出函数f(x)的单调区间(无需证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得aman=16a12 , 则
 +
+  的最小值为( )
的最小值为( )
A.
B.
C.
D.不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】2012年,商品价格一度成为社会热点话题,某种新产品投放市场的100天中,前40天价格呈直线上升,由于政府及时采取有效措施,从而使后60天的价格呈直线下降,现统计出其中4天的价格如下表
时间
第4天
第32天
第60天
第90天
价格(元)
23
30
22
7
(1)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天);
(2)销售量g(x)与时间x的函数关系: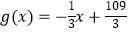 (1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元?
(1≤x≤100,且x∈N),则该产品投放市场第几天销售额最高?最高为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=
 ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A.AC⊥BF
B.直线AE,BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值
相关试题