【题目】已知函数f(x)=|x﹣2|﹣|2x﹣a|,a∈R.
(1)当a=3时,解不等式f(x)>0;
(2)当x∈(﹣∞,2)时,f(x)<0恒成立,求a的取值范围.
参考答案:
【答案】
(1)解:f(x)= 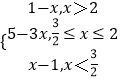 ,
,
当x>2时,1﹣x>0,即x<1,解得x∈;
当 ![]() ≤x≤2时,5﹣3x>0,即x<
≤x≤2时,5﹣3x>0,即x< ![]() ,解得
,解得 ![]() ≤x<
≤x< ![]() ;
;
当x< ![]() 时,x﹣1>0,即x>1,解得1<x<
时,x﹣1>0,即x>1,解得1<x< ![]() ;
;
综上所述,不等式的解集为{x|1<x< ![]() }
}
(2)解:当x∈(﹣∞,2)时,f(x)<0恒成立2﹣x﹣|2x﹣a|<0
2﹣x<|2x﹣a|恒成立
2﹣x<2x﹣a或2x﹣a<x﹣2恒成立
x> ![]() 或x<a﹣2恒成立,
或x<a﹣2恒成立,
∴当x∈(﹣∞,2)时,a<3x﹣2①或a>x+2②恒成立,
解①,a不存在;解②得:a≥4.
综上知,a≥4
【解析】(1)依题意知,a=3时,f(x)= 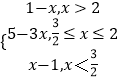 ,通过对x范围的分类讨论,解不等式f(x)>0即可;(2)利用等价转化的思想,通过分离参数a,可知当x∈(﹣∞,2)时,a<3x﹣2或a>x+2恒成立,从而可求得a的取值范围.
,通过对x范围的分类讨论,解不等式f(x)>0即可;(2)利用等价转化的思想,通过分离参数a,可知当x∈(﹣∞,2)时,a<3x﹣2或a>x+2恒成立,从而可求得a的取值范围.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
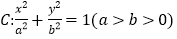 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+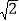 =0相切.
=0相切.(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于两点A,B,当
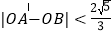 时,求直线斜率的取值范围.
时,求直线斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在区间
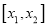 上的函数
上的函数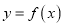 的图象为
的图象为 ,
, 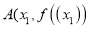 、
、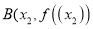 ,且
,且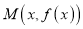 为图象
为图象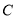 上的任意一点,
上的任意一点, 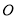 为坐标原点,当实数
为坐标原点,当实数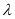 满足
满足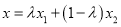 时,记向量
时,记向量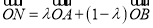 ,若
,若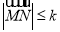 恒成立,则称函数
恒成立,则称函数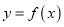 在区间
在区间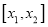 上可在标准
上可在标准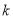 下线性近似,其中
下线性近似,其中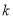 是一个确定的正数.
是一个确定的正数.(1)设函数
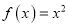 在区间
在区间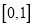 上可在标准
上可在标准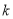 下线性近似,求
下线性近似,求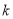 的取值范围;
的取值范围;(2)已知函数
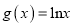 的反函数为
的反函数为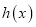 ,函数
,函数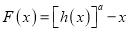 ,(
,( 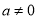 ),点
),点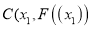 、
、 ,记直线
,记直线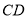 的斜率为
的斜率为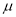 ,若
,若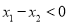 ,问:是否存在
,问:是否存在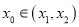 ,使
,使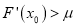 成立?若存在,求
成立?若存在,求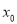 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一支车队有
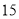 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午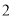 时出发,第二辆车于下午
时出发,第二辆车于下午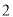 时
时 分出发,第三辆车于下午
分出发,第三辆车于下午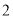 时
时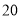 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午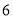 时停下来休息.
时停下来休息.到下午
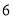 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?如果每辆车的行驶速度都是
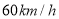 ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少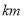 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,角A,B,C的对边分别是a,b,c,且2cos2
 =
= 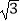 sinB,a=3c.
sinB,a=3c.
(1)求角B的大小和tanC的值;
(2)若b=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
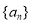 的前
的前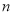 项和为
项和为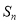 ,
, 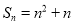 ,数列
,数列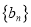 的通项公式为
的通项公式为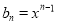 .
.(1)求数列
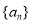 的通项公式;
的通项公式;(2)设
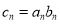 ,数列
,数列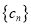 的前
的前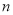 项和为
项和为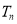 ,
,①求
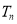 ;
;②若
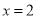 ,求数列
,求数列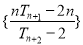 的最小项的值.
的最小项的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是公差为2的等差数列,且a1 , a4 , a13成等比数列,数列{
 }是首项为1,公比为3的等比数列.
}是首项为1,公比为3的等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设数列{an+bn}的前n项和Rn , 若不等式 ≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
相关试题

