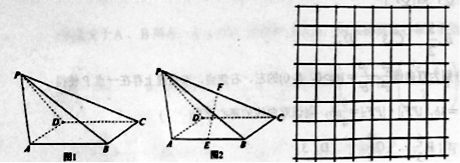
【题目】如图1,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() .
.
(1)如图2,设点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)已知网格纸上小正方形的边长为![]() ,请你在网格纸上用粗线画图1中四棱锥
,请你在网格纸上用粗线画图1中四棱锥![]() 的府视图(不需要标字母),并说明理由.
的府视图(不需要标字母),并说明理由.
参考答案:
【答案】(1)证明见解析;(2)俯视图见解析.
【解析】
试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,得到
的中点,得到![]() ,再根据中位线得到
,再根据中位线得到![]() ,即可利用线面平行的判定定理,证得结论;(2)由
,即可利用线面平行的判定定理,证得结论;(2)由![]() ,得
,得![]() ,得到底面
,得到底面![]() 是正方形,进而得到
是正方形,进而得到![]() 平面
平面![]() 即可求解三视图的俯视图.
即可求解三视图的俯视图.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中位线,
的中位线,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
![]() 是矩形
是矩形![]() 的中位线,
的中位线,![]() 面
面![]() 与
与![]() 相交,
相交,
![]() 面
面![]() 面
面![]() 面
面![]() 平面
平面![]() .
.
(2)![]() 底面
底面![]() 是正方形,
是正方形,![]() 平面
平面![]()
![]() 在平面
在平面![]() 的射影
的射影![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,
府视图如图所示,

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列
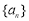 中,已知
中,已知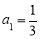 ,
,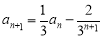 ,
,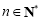 ,设
,设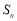 为
为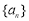 的前
的前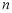 项和.
项和.(1)求证:数列
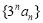 是等差数列;
是等差数列;(2)求
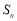 ;
;(3)是否存在正整数
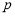 ,
,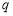 ,
,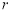
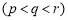 ,使
,使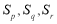 成等差数列?若存在,求出
成等差数列?若存在,求出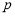 ,
,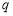 ,
,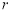 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,  ,
,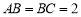 ,
, 为
为 的中点.
的中点.(1)求异面直线
 ,
, 所成角的余弦值;
所成角的余弦值;(2)点
 在线段
在线段 上,且
上,且 ,若直线
,若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市有一直角梯形绿地
 ,其中
,其中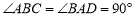 ,
, km,
km,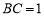 km.现过边界
km.现过边界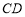 上的点
上的点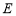 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管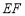 ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.(1)如图①,若
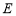 为
为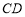 的中点,
的中点,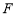 在边界
在边界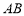 上,求灌溉水管
上,求灌溉水管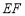 的长度;
的长度;(2)如图②,若
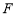 在边界
在边界 上,求灌溉水管
上,求灌溉水管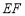 的最短长度.
的最短长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
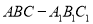 中,侧棱垂直于底面,
中,侧棱垂直于底面,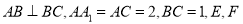 分别是
分别是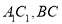 的中点.
的中点.(1)求证: 平面
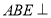 平面
平面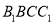 ;
;(2)求证:
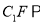 平面
平面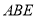 ;
; (3)求三棱锥
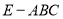 体积.
体积.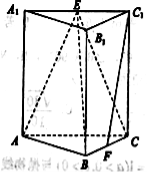
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱
 中,已知
中,已知 ,
, 分别为
分别为 ,
, 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .求证:
.求证:(1)直线
 ∥平面
∥平面 ;
;(2)直线
 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,已知圆
中,已知圆 及点
及点 ,
, .
.(1)若直线
 平行于
平行于 ,与圆
,与圆 相交于
相交于 ,
, 两点,
两点, ,求直线
,求直线 的方程;
的方程;(2)在圆
 上是否存在点
上是否存在点 ,使得
,使得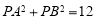 ?若存在,求点
?若存在,求点 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
相关试题

