【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
参考答案:
【答案】(1)f(x)=22-x-1,x∈[1,2];(2)1.
【解析】试题分析:(1) ![]() ;(2) 有对称性和奇偶性可得
;(2) 有对称性和奇偶性可得![]()
![]() 所求
所求![]() .
.
试题解析:
(1)当x∈[1,2]时,2-x∈[0,1],
又f(x)的图象关于x=1对称,
则f(x)=f(2-x)=22-x-1,x∈[1,2].
(2)∵函数f(x)为奇函数,则f(-x)=-f(x),
又函数f(x)的图象关于x=1对称,
则f(2+x)=f(-x)=-f(x),
所以f(4+x)=f[(2+x)+2]=-f(2+x)=f(x),
所以f(x)是以4为周期的周期函数.
∵f(0)=0,f(1)=1,f(2)=0,f(3)=f(-1)=-f(1)=-1,
又f(x)是以4为周期的周期函数.
∴f(0)+f(1)+f(2)+…+f(2017)=504×(0+1+0-1)+f(0)+f(1)=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示没有命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. 0.35 B. 0.25
C. 0,20 D. 0.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在常数
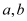 ,使等式
,使等式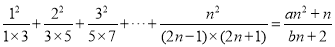 对于一切
对于一切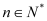 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 在(1,+∞)上的单调性,并用定义证明你的结论;
在(1,+∞)上的单调性,并用定义证明你的结论;(3)若
 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
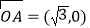 ,
,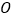 为坐标原点,动点
为坐标原点,动点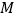 满足:
满足: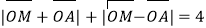 .
.(Ⅰ)求动点
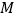 的轨迹
的轨迹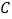 的方程;
的方程;(Ⅱ)已知直线
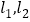 都过点
都过点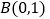 ,且
,且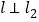 ,
,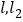 与轨迹
与轨迹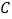 分别交于点
分别交于点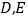 ,试探究是否存在这样的直线?使得
,试探究是否存在这样的直线?使得 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】据市场分析,南雄市精细化工园某公司生产一种化工产品,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.写出月总成本y(万元)关于月产量x(吨)的函数关系.已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
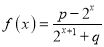 的定义域为
的定义域为 ,且
,且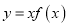 是偶函数.
是偶函数.(1)求实数
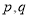 的值;
的值;(2)证明:函数
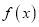 在
在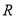 上是减函数;
上是减函数;(3)当
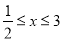 时,
时, 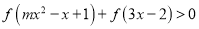 恒成立,求实数
恒成立,求实数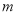 的取值范围.
的取值范围.
相关试题

