【题目】已知向量![]() ,
,![]() 为坐标原点,动点
为坐标原点,动点![]() 满足:
满足:![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 都过点
都过点![]() ,且
,且![]() ,
,![]() 与轨迹
与轨迹![]() 分别交于点
分别交于点![]() ,试探究是否存在这样的直线?使得
,试探究是否存在这样的直线?使得![]() 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
参考答案:
【答案】设点![]() ,则
,则![]() …… 1分
…… 1分
∵![]()
∴![]() ……… ……… ……… 2分
……… ……… ……… 2分
∴点M的轨迹C是以![]() 为焦点,长轴长为 4 的椭圆……… …… ……… 4分
为焦点,长轴长为 4 的椭圆……… …… ……… 4分
∴![]() ∴
∴![]()
∴ 动点M的轨迹C的方程为![]() ……… ……… ……… 6分
……… ……… ……… 6分
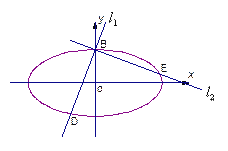
(2)由(1)知,轨迹C是椭圆![]() ,点
,点![]() 是它的上顶点,
是它的上顶点,
设满足条件的直线![]() 、
、![]() 存在,直线
存在,直线![]() 的方程为
的方程为![]() ①
①
则直线![]() 的方程为
的方程为![]() ,② ……… ……… ……… 7分
,② ……… ……… ……… 7分
将①代入椭圆方程并整理得:![]() ,可得
,可得![]() ,则
,则![]() .
.
将②代入椭圆方程并整理得:![]() ,可得
,可得![]() ,则
,则![]() .
.
由△BDE是等腰直角三角形得![]()
![]()
![]()
![]()
![]()
![]()
![]() …………11分
…………11分
∴![]() 或
或![]() ④…………………………………………12分
④…………………………………………12分
∵方程④![]() 或
或![]() .
.
∴即满足条件的直线![]() 、
、![]() 存在,共有3组.
存在,共有3组.
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在常数
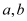 ,使等式
,使等式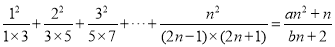 对于一切
对于一切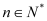 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 在(1,+∞)上的单调性,并用定义证明你的结论;
在(1,+∞)上的单调性,并用定义证明你的结论;(3)若
 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据市场分析,南雄市精细化工园某公司生产一种化工产品,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.写出月总成本y(万元)关于月产量x(吨)的函数关系.已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
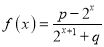 的定义域为
的定义域为 ,且
,且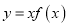 是偶函数.
是偶函数.(1)求实数
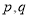 的值;
的值;(2)证明:函数
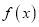 在
在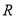 上是减函数;
上是减函数;(3)当
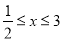 时,
时, 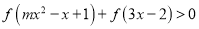 恒成立,求实数
恒成立,求实数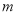 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】社会公众人物的言行一定程度上影响着年轻人的人生观、价值观.某媒体机构为了解大学生对影视、歌星以及著名主持人方面的新闻(简称:“星闻”)的关注情况,随机调查了某大学的
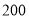 位大学生,得到信息如下表:
位大学生,得到信息如下表: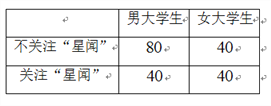
(Ⅰ)从所抽取的
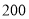 人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;(Ⅱ)是否有
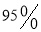 以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
以上的把握认为“关注‘星闻’与性别有关”,并说明理由; (Ⅲ)把以上的频率视为概率,若从该大学随机抽取
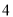 位男大学生,设这
位男大学生,设这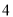 人中关注“星闻”的人数为
人中关注“星闻”的人数为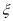 ,求
,求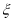 的分布列及数学期望.
的分布列及数学期望.附:
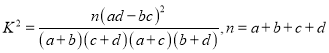 .
.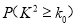
0.050
0.010
0.001
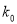
3.841
6.635
10.828
相关试题

