【题目】是否存在常数![]() ,使等式
,使等式![]() 对于一切
对于一切![]() 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
参考答案:
【答案】![]() ,证明详见解析.
,证明详见解析.
【解析】
试题分析:先从特殊情形![]() ,等式必须成立,求出
,等式必须成立,求出![]() 值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
试题解析:若存在常数![]() 使等式成立,则将
使等式成立,则将![]() 代入上式,有
代入上式,有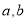 得
得![]() ,即有
,即有 ![]() 对于一切
对于一切![]() 成立. 5分
成立. 5分
数学归纳法证明如下:
证明如下:(1)当![]() 时,左边=
时,左边=![]() ,右边=
,右边=![]() ,所以等式成立,
,所以等式成立,
(2)假设![]() (
(![]() 且
且![]() )时等式成立,即
)时等式成立,即![]() ,
,
当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]()
![]()
也就是说,当![]() 时,等式成立,
时,等式成立,
综上所述,可知等式对任何![]() 都成立. 12分
都成立. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个正数a,b,可按规则
 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为
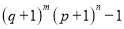 (m,n为正整数),
(m,n为正整数),则m,n的值分别为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
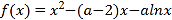 .
.(1)求函数
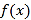 的单调区间;
的单调区间;(2)若函数
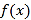 有两个零点,求满足条件的最小正整数
有两个零点,求满足条件的最小正整数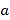 的值;
的值;(3)若方程
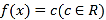 ,有两个不相等的实数根
,有两个不相等的实数根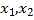 ,比较
,比较 与0的大小.
与0的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示没有命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. 0.35 B. 0.25
C. 0,20 D. 0.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 在(1,+∞)上的单调性,并用定义证明你的结论;
在(1,+∞)上的单调性,并用定义证明你的结论;(3)若
 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
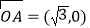 ,
, 为坐标原点,动点
为坐标原点,动点 满足:
满足: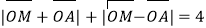 .
.(Ⅰ)求动点
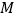 的轨迹
的轨迹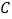 的方程;
的方程;(Ⅱ)已知直线
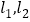 都过点
都过点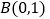 ,且
,且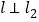 ,
,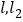 与轨迹
与轨迹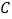 分别交于点
分别交于点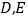 ,试探究是否存在这样的直线?使得
,试探究是否存在这样的直线?使得 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
相关试题

