搜索
【题目】过点M（﹣2，0）的直线l与椭圆x2+2y2=2交于P1 ， P2 ， 线段P1P2的中点为P．设直线l的斜率为k1（k1≠0），直线OP的斜率为k2 ， 则k1k2等于（ ）
A.﹣2
B.2
C.
D.﹣
参考答案：
【答案】D
【解析】解：设直线l的方程为
y=k1（x+2），代入x2+2y2=2，得（1+2k12）x2+8k12x+8k12﹣2=0，所以x1+x2=﹣ 
，
而y1+y2=k1（x1+x2+4）= 
，
所以OP的斜率k2= 
=﹣ 
，
所以k1k2=﹣ 
，
故选D．
设直线l的方程为y=k1（x+2），代入x2+2y2=2，得（1+2k12）x2+8k12x+8k12﹣2=0，然后由根与系数的关系求解能够得到k1k2的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x|x﹣a|+2x．
（1）若函数f（x）在R上是增函数，求实数a的取值范围；
（2）求所有的实数a，使得对任意x∈[1，2]时，函数f（x）的图象恒在函数g（x）=2x+1图象的下方；
（3）若存在a∈[﹣4，4]，使得关于x的方程f（x）=tf（a）有三个不相等的实数根，求实数t的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y2=4
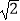x的交点为椭圆 
（a＞b＞0）的右焦点，且椭圆的长轴长为4，左右顶点分别为A，B，经过椭圆左焦点的直线l与椭圆交于C，D（异于A，B）两点．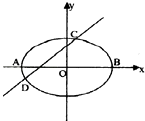 
（1）求椭圆标准方程；
（2）求四边形ADBC的面积的最大值；
（3）若M（x1 ， y1）N（x2 ， y2）是椭圆上的两动点，且满x1x2+2y1y2=0，动点P满足
（其中O为坐标原点），是否存在两定点F1 ， F2使得|PF1|+|PF2|为定值，若存在求出该定值，若不存在说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】将函数f（x）=sin（2x+φ）（0＜φ＜π）的图象向左平移
个单位后得到函数y=g（x）的图象，若y=g（x）是偶函数，则φ= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知E，F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC，CC1的中点，则截面AEFD1与底面ABCD所成二面角的正弦值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知集合A={x|f（x）=lg（x﹣1）+
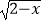}，集合B={y|y=2x+a，x≤0}．
（1）若a=
，求A∪B；
（2）若A∩B=，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知过抛物线y2=2px（p＞0）的焦点，斜率为2
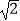的直线交抛物线于A（x1 ， y1）和B（x2 ， y2）（x1＜x2）两点，且|AB|=9，
（1）求该抛物线的方程；
（2）O为坐标原点，C为抛物线上一点，若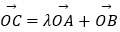
，求λ的值．
相关试题
