【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点.
的中点.

(1)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置并证明结论;若不存在,请说明理由.
的位置并证明结论;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 为中点
为中点
【解析】
试题分析:(1)如图建系![]() .分别求出平面
.分别求出平面![]() ,
,![]() 的一个法向量,利用两法向量的夹角求解;(2)设
的一个法向量,利用两法向量的夹角求解;(2)设![]() ,欲使
,欲使![]() 平面
平面![]() ,当且仅当
,当且仅当![]() ,列出关于
,列出关于![]() 的方程并求解即可.
的方程并求解即可.
试题解析:(1)![]() 为直三棱柱,
为直三棱柱,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 建立如图所示的空间直角坐标系,则
建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .设平面
.设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则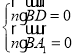 ,即
,即![]() ,得
,得![]() ,
,![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,
由图可知,二面角![]() 的平面角为锐角,
的平面角为锐角,
![]() 二面角
二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.
(2)在线段![]() 上存在一点
上存在一点![]() ,设为
,设为![]() ,使得
,使得![]() 平面
平面![]() .
.
欲使![]() 平面
平面![]() ,由(1)知,当且仅当
,由(1)知,当且仅当![]() .
.
![]() ,
,![]() .
.
![]() 在线段
在线段![]() 上存在一点
上存在一点![]() 满足条件,此时点
满足条件,此时点![]() 为
为![]() 的中点.
的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个人打靶时连续射击两次,则事件“恰有一次中靶”的互斥的事件是( )
A. 至多有一次中靶 B. 两次都中靶
C. 恰有一次不中靶 D. 至少有一次中靶
-
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在
 上的函数
上的函数
 ,函数
,函数 ,当
,当 时,
时, 取得极大值
取得极大值 ,且函数
,且函数
的图象关于点
 对称.
对称.(1)求函数
 的表达式;
的表达式;(2)求证:当
 时,
时, 为自然对数的底数);
为自然对数的底数);(3)若
 ,数列
,数列 中是否存在
中是否存在 ?若存在,求出所有相等的两项,若不存在,说明理由.
?若存在,求出所有相等的两项,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求证:函数
时,求证:函数 的图像关于点
的图像关于点 对称;
对称;(Ⅱ)当
 时,求
时,求 的单调区间.
的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面几何中的三角形在立体几何中类比的对象是( )
A.三棱柱 B.三棱台 C.三棱锥 D.正方体
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列{an}中,a2 020=8a2 017,则公比q的值为( ).
A. 2 B. 3 C. 4 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
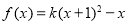 ,
,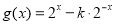 (
(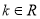 且
且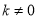 ).
).(1)若
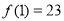 ,求函数
,求函数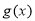 在区间
在区间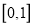 上的值域;
上的值域;(2)当
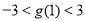 时,函数
时,函数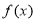 在区间
在区间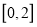 上的最小值大于
上的最小值大于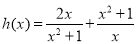 在
在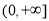 上的最小值,求实数
上的最小值,求实数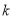 的取值范围.
的取值范围.
相关试题

