【题目】设定义在![]() 上的函数
上的函数![]()
![]() ,函数
,函数![]() ,当
,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,且函数
,且函数![]()
的图象关于点![]() 对称.
对称.
(1)求函数![]() 的表达式;
的表达式;
(2)求证:当![]() 时,
时, 为自然对数的底数);
为自然对数的底数);
(3)若![]() ,数列
,数列![]() 中是否存在
中是否存在![]() ?若存在,求出所有相等的两项,若不存在,说明理由.
?若存在,求出所有相等的两项,若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)存在,
;(2)证明见解析;(3)存在,![]()
【解析】
试题分析:(1)函数![]() 的图象关于点
的图象关于点![]() 对称,则函数
对称,则函数![]() 的图象关于点
的图象关于点![]() 对称,即函数
对称,即函数![]() 是奇函数.再结合当
是奇函数.再结合当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,导数为零,可求得
,导数为零,可求得![]() ;(2)由(1)知
;(2)由(1)知![]() 当
当![]() 时不等式
时不等式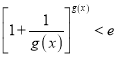 即为:
即为: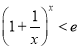 ,等价于
,等价于![]() ,构造函数
,构造函数![]() ,利用导数证明函数
,利用导数证明函数![]() 在
在![]() 上是减函数,故有
上是减函数,故有![]() 时,
时,![]() 成立, 用
成立, 用![]() 代换
代换![]() 得:
得:![]() 时,
时,![]() 成立;(3)依题意
成立;(3)依题意![]() ,利用特殊项可知
,利用特殊项可知![]() ,利用商比较法证明
,利用商比较法证明![]() 的单调性,由此求得
的单调性,由此求得![]() 是唯一结果.
是唯一结果.
试题解析:
(1)将函数![]() 的图象向右平移一个单位,得到函数
的图象向右平移一个单位,得到函数![]() 的图象,
的图象,![]() 函数
函数![]() 的图象关于点
的图象关于点![]() 对称,即函数
对称,即函数![]() 是奇函数,
是奇函数,![]() ,
,
由题意得: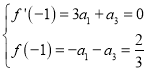 ,所以
,所以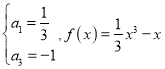 ,经检验满足题意.
,经检验满足题意.
(2)由(1)知![]() 当
当![]() 时不等式
时不等式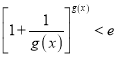 即为:
即为:![]() ,构造函数
,构造函数![]() ,
,
则![]() ,所以函数
,所以函数![]() 在
在![]() 上是减函数, 因而
上是减函数, 因而![]() 时,
时,![]() ,即:
,即:![]() 时,
时,![]() 成立,用
成立,用![]() 代换
代换![]() 得:
得:![]() 时,
时,![]() 成立,所以
成立,所以![]() 时,
时,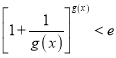 成立.
成立.
(3)![]() ,则由(2)知:
,则由(2)知: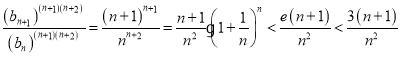 ,
,
令![]() ,得:
,得:![]() ,结合
,结合![]() 得:
得:![]() ,因此,当
,因此,当![]() 时,有
时,有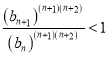 ,所以当
,所以当![]() 时,
时,![]() ,即:
,即:![]() ,又通过比较
,又通过比较![]() 的大小知:
的大小知:![]() ,因为
,因为![]() ,且
,且![]() 时
时![]() ,所以若数列
,所以若数列![]() 中存在相等的两项,只能是
中存在相等的两项,只能是![]() 、
、![]() 与后面的项可能相等,又
与后面的项可能相等,又![]() ,所以数列
,所以数列![]() 中存在唯一相等的两项,即:
中存在唯一相等的两项,即:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)讨论
 的单调性;
的单调性;(2)当
 时,证明:
时,证明: 对于任意的
对于任意的 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】从编号为1~50的50枚最新研制的某种型号的导弹中随机抽取5枚进行发射实验,若采用每部分选取的号码间隔一样的系统抽样方法,则所选取5枚导弹的编号可能是( )
A. 5,10,15,20,25
B. 3,13,23,33,43
C. 1,2,3,4,5
D. 2,4,8,16,32
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个人打靶时连续射击两次,则事件“恰有一次中靶”的互斥的事件是( )
A. 至多有一次中靶 B. 两次都中靶
C. 恰有一次不中靶 D. 至少有一次中靶
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求证:函数
时,求证:函数 的图像关于点
的图像关于点 对称;
对称;(Ⅱ)当
 时,求
时,求 的单调区间.
的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, ,
, ,
, 分别为棱
分别为棱 的中点.
的中点.
(1)求二面角
 的平面角的余弦值;
的平面角的余弦值;(2)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?若存在,确定点
?若存在,确定点 的位置并证明结论;若不存在,请说明理由.
的位置并证明结论;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面几何中的三角形在立体几何中类比的对象是( )
A.三棱柱 B.三棱台 C.三棱锥 D.正方体
相关试题

