【题目】在![]() 中,三内角A,B,C的对边分别为a,b,c.
中,三内角A,B,C的对边分别为a,b,c.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,且
,且![]() 为钝角,证明:
为钝角,证明: ![]() ,并求
,并求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,(2)
,(2)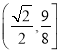
【解析】试题分析:
(1)由题意结合正弦定理可得![]() 或
或![]() ,结合两角和差正余弦公式可得
,结合两角和差正余弦公式可得![]() ;
;
(2)利用题意得到关于sinA的二次函数,结合二次函数的性质可得![]() 的取值范围是
的取值范围是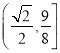 .
.
试题解析:
(1)由正弦定理可得![]() ,
,
∵c![]() ,A=45°,a=2,
,A=45°,a=2,
∴sinC=![]() ,
,
∴C=60°或120°,
由正弦定理可得![]()
当C=60°,sinB=sin(A+C)=sin45°cos60°+cos45°sin60°=![]()
∴b=![]() ,
,
当C=120°,sinB=sin(A+C)=sin45°cos120°+cos45°sin120°=![]()
∴b=![]() ,
,
(2)由题意得a=btanA,
∴由正弦定理得![]() ,则sinB=cosA,
,则sinB=cosA,
∵B为钝角,∴![]() ,
,
∴BA=![]() ;
;
∴C=π(A+B)=π(A+![]() +A)=
+A)= ![]() 2A>0,
2A>0,
∴A∈(0, ![]() ),
),
∴sinA+sinC=sinA+sin(![]() 2A)=sinA+cos2A=sinA+12sin/span>2A=2(sinA
2A)=sinA+cos2A=sinA+12sin/span>2A=2(sinA![]() )2+
)2+![]() ,
,
∵A∈(0, ![]() ),∴0<sinA<
),∴0<sinA<![]() ,
,
∴由二次函数可知, ![]() ,
,
∴sinA+sinC的取值范围为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
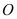 是坐标原点,若椭圆
是坐标原点,若椭圆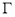 :
: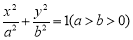 的离心率为
的离心率为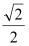 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为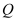 ,
,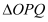 的面积为
的面积为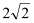 .
.(1)求椭圆
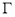 的标准方程;
的标准方程;(2)已知点
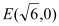 ,
,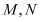 为椭圆
为椭圆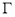 上两动点,若有
上两动点,若有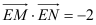 ,证明:直线
,证明:直线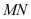 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用
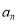 的信息如下图.
的信息如下图.
(1)求
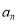 ;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(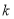 为常数,
为常数,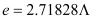 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点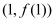 处的切线与
处的切线与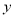 轴垂直.
轴垂直.(1)求
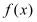 的单调区间;
的单调区间;(2)设
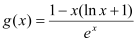 ,对任意
,对任意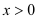 ,证明:
,证明: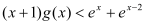 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为
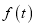 (单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设
(单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设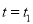 时,乙到达C地.
时,乙到达C地.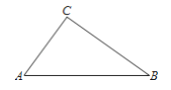
(1)求
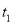 与
与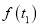 的值;
的值;(2)已知警员的对讲机的有效通话距离是3千米.当
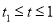 时,求
时,求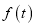 的表达式,并判断
的表达式,并判断 在
在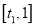 上的最大值是否超过3?并说明理由.
上的最大值是否超过3?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
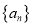 的前
的前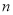 项和为
项和为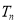 ,且
,且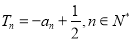 ,设
,设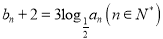 ,数列
,数列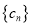 满足
满足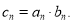 .
.(1)求数列
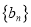 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和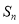 ;
;(3)若
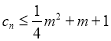 对一切正整数
对一切正整数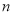 恒成立,求实数
恒成立,求实数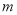 的取值范围.
的取值范围.
相关试题

