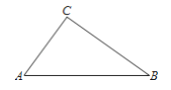
【题目】如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为![]() (单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设
(单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设![]() 时,乙到达C地.
时,乙到达C地.
(1)求![]() 与
与![]() 的值;
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当![]() 时,求
时,求![]() 的表达式,并判断
的表达式,并判断![]() 在
在![]() 上的最大值是否超过3?并说明理由.
上的最大值是否超过3?并说明理由.
参考答案:
【答案】(1) ![]() 千米;(2)f(t)的最大值没有超过3千米。
千米;(2)f(t)的最大值没有超过3千米。
【解析】试题分析:
(1)有题意可得![]() ,然后结合余弦定理可得
,然后结合余弦定理可得![]() 千米;
千米;
(2)利用题意结合二次函数和分段函数的性质可得f(t)的最大值没有超过3千米。
试题解析:
(1)由题意可得![]() ,
,
设此时甲运动到点P,则![]() 千米,
千米,
∴![]() =
=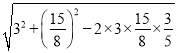 =
=![]() 千米;
千米;
(2)当![]() 时,乙在CB上的Q点,设甲在P点,
时,乙在CB上的Q点,设甲在P点,
∴QB=AC+CB8t=78t,PB=ABAP=55t,
∴f(t)=PQ=![]() =
=![]() =
=![]() ,
,
当![]() 时,乙在B点不动,设此时甲在点P,
时,乙在B点不动,设此时甲在点P,
∴f(t)=PB=ABAP=55t
∴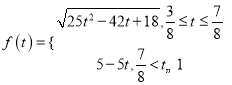 ,
,
∴当![]() 时,
时, 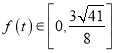 ,
,
故f(t)的最大值没有超过3千米。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用
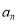 的信息如下图.
的信息如下图.
(1)求
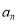 ;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,三内角A,B,C的对边分别为a,b,c.
中,三内角A,B,C的对边分别为a,b,c.(1)若
 ,求
,求 ;
;(2)若
 ,且
,且 为钝角,证明:
为钝角,证明:  ,并求
,并求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(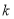 为常数,
为常数,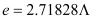 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点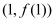 处的切线与
处的切线与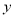 轴垂直.
轴垂直.(1)求
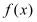 的单调区间;
的单调区间;(2)设
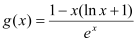 ,对任意
,对任意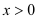 ,证明:
,证明: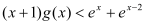 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
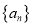 的前
的前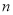 项和为
项和为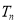 ,且
,且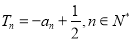 ,设
,设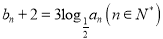 ,数列
,数列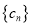 满足
满足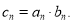 .
.(1)求数列
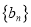 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和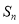 ;
;(3)若
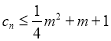 对一切正整数
对一切正整数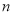 恒成立,求实数
恒成立,求实数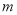 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为
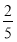 ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为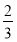 ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为
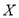 ,求
,求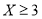 的概率;
的概率;(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为
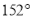 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为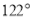 .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为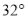 .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.
相关试题

