【题目】已知函数![]() ,下列命题正确的有_______.(写出所有正确命题的编号)
,下列命题正确的有_______.(写出所有正确命题的编号)
①![]() 是奇函数;
是奇函数;
②![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
③方程![]() 有且仅有1个实数根;
有且仅有1个实数根;
④如果对任意![]() ,都有
,都有![]() ,那么
,那么![]() 的最大值为2.
的最大值为2.
参考答案:
【答案】①②④
【解析】分析:用奇函数的定义判断![]() 是否为奇函数,由导数证明函数的单调性,由零点存在定理及零点的定义确定零点的个数是否为1,利用导数求出函数的最值确定参数的范围.
是否为奇函数,由导数证明函数的单调性,由零点存在定理及零点的定义确定零点的个数是否为1,利用导数求出函数的最值确定参数的范围.
详解:![]() ,∴
,∴![]() 是奇函数,①正确;
是奇函数,①正确;
![]() ,∴
,∴![]() 是
是![]() 上的增函数,②正确
上的增函数,②正确
设![]() ,易知
,易知![]() ,0是
,0是![]() 的一个零点,
的一个零点,![]() ,而
,而![]() ,即
,即![]() 在
在![]() 上也存在零点,
上也存在零点,
∴![]() 的零点多至少有2个,③错;
的零点多至少有2个,③错;
设![]() ,则
,则![]() ,易知
,易知![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增,又
单调递增,又![]() ,∴当
,∴当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,因此存在
,因此存在![]() ,使
,使![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上不恒成立,综上
上不恒成立,综上![]()
![]() ,即
,即![]() 的最大值为2,④正确.
的最大值为2,④正确.
故答案为①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=2cos2x的图象向右平移
 个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
个单位后得到函数g(x)的图象,若函数g(x)在区间[0,  ]和[2a,
]和[2a,  ]上均单调递增,则实数a的取值范围是( )
]上均单调递增,则实数a的取值范围是( )
A.[ ,
,  ]
]
B.[ ,
,  ]
]
C.[ ,
,  ]
]
D.[ ,
, 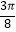 ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Sn为数列{an}的前n项和,且满足Sn﹣2an=n﹣4.
(1)证明{Sn﹣n+2}为等比数列;
(2)设数列{Sn}的前n项和Tn , 比较Tn与2n+2﹣5n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】为利于分层教学,某学校根据学生的情况分成了A,B,C三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成缎,其统计表如下:
A类
第x次
1
2
3
4
4
分数y(满足150)
145
83
95
72
110
 ,
, ;
;B类
第x次
1
2
3
4
4
分数y(满足150)
85
93
90
76
101
 ,
, ;
;C类
第x次
1
2
3
4
4
分数y(满足150)
85
92
101
100
112
 ,
, ;
;(1)经计算己知A,B的相关系数分别为
 ,
, .,请计算出C学生的
.,请计算出C学生的 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留两位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留两位有效数字, 越大认为成绩越稳定)
越大认为成绩越稳定)(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归直线方程为
 ,利用线性回归直线方程预测该生第十次的成绩.
,利用线性回归直线方程预测该生第十次的成绩.附相关系数
 ,线性回归直线方程
,线性回归直线方程 ,
, ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数
 描述一年中入住客栈的游客人数y与月x份之间的关系;
描述一年中入住客栈的游客人数y与月x份之间的关系;(2)请问哪几个月份要准备400份以上的食物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一矩形花坛
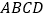 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上, 点在
点在 上,且对角线
上,且对角线 过
过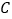 点,已知
点,已知 米,
米, 米.
米.
(1)要使矩形
 的面积大于
的面积大于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?(2)当
 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
相关试题

