【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
参考答案:
【答案】
(1)解:圆的方程化为(x﹣1)2+(y﹣2)2=5﹣m,
圆心 C(1,2),半径 ![]() ,
,
则圆心C(1,2)到直线l:x+2y﹣4=0的距离为:
![]()
由于 ![]() ,则
,则 ![]() ,
,
有 ![]() ,
,
∴ ![]() ,解得m=4.
,解得m=4.
(2)假设存在直线l:x﹣2y+c=0,
使得圆上有四点到直线l的距离为 ![]() ,
,
由于圆心 C(1,2),半径r=1,
则圆心C(1,2)到直线l:x﹣2y+c=0的距离为:
![]() ,
,
解得 ![]() .
.
【解析】(1)由圆与直线相交于M,N两点,圆心到直线的距离令为d,构照直角三角形即可求出m。
(2)若存在直线l,使得圆上有四点到直线l的距离为![]() ,则圆心到直线的距离
,则圆心到直线的距离![]() 即可求出答案。
即可求出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)设各项均为正数的等比数列
 中,
中,

(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求证:
,求证:  ;
;(3)是否存在正整数
 ,使得
,使得 对任意正整数
对任意正整数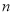 均成立?若存在,求出
均成立?若存在,求出 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲船在岛
 的正南方
的正南方 处,
处, 千米,甲船以每小时
千米,甲船以每小时 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自 出发以每小时
出发以每小时 千米的速度向北偏东
千米的速度向北偏东 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )A.
 分钟 B.
分钟 B.  分钟 C.
分钟 C.  分钟 D.
分钟 D.  分钟
分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ,
,  )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某高校大学5000名新生的视力情况,随机地抽查了该校100名进校新生的视力情况,得到其频率分布直方图如右图,若规定视力低于5.0的学生属[于近视学生,则估计该校新生中不是近视的人数约为( )

A.300人
B.400人
C.600人
D.1000人 -
科目: 来源: 题型:
查看答案和解析>>【题目】某小朋友按如下规则练习数数,
 大拇指,
大拇指, 食指,
食指, 中指,
中指, 无名指,
无名指, 小指,
小指, 无名指,
无名指,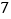 中指,
中指, 食指,
食指, 大拇指,
大拇指, 食指,
食指, ,一直数到
,一直数到 时,对应的指头是( )
时,对应的指头是( )
A. 小指 B. 中指 C. 食指 D. 无名指
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批产品抽50件测试,其净重介于13克与19克之间,将测试结果按如下方式分成六组:第一组,净重大于等于13克且小于14克;第二组,净重大于等于14克且小于15克;…第六组,净重大于等于18克且小于19克.如图是按上述分组方法得到的频率分布直方图.设净重小于17克的产品数占抽取数的百分比为x,净重大于等于15克且小于17克的产品数为y,则从频率分布直方图中可分析出x和y分别为( )

A.0.9,35
B.0.9,45
C.0.1,35
D.0.1,45
相关试题

