【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行![]() 天试销,每种单价试销
天试销,每种单价试销![]() 天,得到如下数据:
天,得到如下数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是![]() 元,
元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:  ,
, ![]()
参考答案:
【答案】(1)10,![]() (2)
(2)![]()
【解析】
试题分析:(1)先求均值,再根据方差公式求方差:![]() ,
,![]() ,根据给出公式求系数
,根据给出公式求系数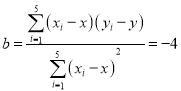 ,再根据回归直线方程过点
,再根据回归直线方程过点![]() 求
求![]() (2)根据利润等于销量乘以单价减去成本得获得的利润
(2)根据利润等于销量乘以单价减去成本得获得的利润![]() ,再根据二次函数最值求法得单价应定为
,再根据二次函数最值求法得单价应定为![]() 元时, 可获得最大利润.
元时, 可获得最大利润.
试题解析:(1)![]() ,
,
![]() ,
,![]() ,
,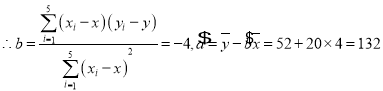 ,所以
,所以![]() 对
对![]() 的回归直线方程为:
的回归直线方程为:![]() .
.
(2)获得的利润![]() ,
,![]() 二次函数
二次函数![]() 的开口朝下,
的开口朝下,
![]() 当
当![]() 时,
时,![]() 取最大值,
取最大值, ![]() 当单价应定为
当单价应定为![]() 元时, 可获得最大利润.
元时, 可获得最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量 (单位:
(单位:  )和年利润
)和年利润 (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费 和年销售量
和年销售量 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

(1)根据散点图判断,
 与
与 哪一个适宜作为年销售量
哪一个适宜作为年销售量 关于年宣传费
关于年宣传费 的回归方程类型?(给出判断即可,不必说出理由);
的回归方程类型?(给出判断即可,不必说出理由);(2)根据(1)的判断结果及表中数据,建立
 关于
关于 的回归方程;
的回归方程;(3)已知这种产品的年利润
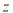 与
与 的关系为
的关系为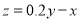 ,根据(2)的结果求:年宣传费
,根据(2)的结果求:年宣传费 为何值时,年利润最大?
为何值时,年利润最大?附:对于一组数据
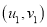 ,
,  ,…
,…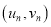 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 上有一个动点
上有一个动点 ,过点
,过点 作直线
作直线 垂直于
垂直于 轴,动点
轴,动点 在
在 上,且满足
上,且满足 (
( 为坐标原点),记点
为坐标原点),记点 的轨迹为
的轨迹为 .
.(I)求曲线
 的方程;
的方程;(II)若直线
 是曲线
是曲线 的一条切线,当点
的一条切线,当点 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富高学生的课外生活,某校要组建数学计算机航空模型3个兴趣小组,小明要选报其中的2个,则包含的样本点共有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C. 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这个两个平面平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
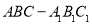 中,
中, ,
, ,平面
,平面 平面
平面 ,
,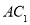 与
与 相交于点
相交于点 .
.
(1)求证:
 ;
;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分,规定满意度不低于98分,则评价该教师为“优秀”,现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶);
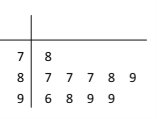
(1)指出这组数据的众数和中位数;
(2)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记
 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求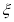 的分布列及数学期望.
的分布列及数学期望.
相关试题

