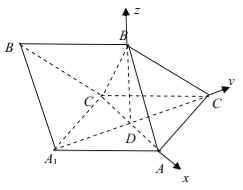
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)首先菱形的性质推出![]() ,然后利用面面垂直的性质推出
,然后利用面面垂直的性质推出![]() 平面
平面![]() ,从而根据线面垂直的性质使问题得证;(2)以
,从而根据线面垂直的性质使问题得证;(2)以![]() 为原点建立空间直角坐标系,然后分别求出相关点的坐标与向量,由此求得平面
为原点建立空间直角坐标系,然后分别求出相关点的坐标与向量,由此求得平面![]() 与平面
与平面![]() 法向量,从而利用空间夹角公式求解即可.
法向量,从而利用空间夹角公式求解即可.
试题解析:(1)已知侧面![]() 是菱形,
是菱形,![]() 是
是![]() 的中点,∵
的中点,∵![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
∴![]() 平面
平面![]() ,
,![]() .
.
(2)如图,以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,由已知可得
轴建立空间直角坐标系,由已知可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量是
的一个法向量是![]() ,
,![]() ,
,![]()
由![]() ,
,![]() ,
,
得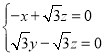 ,可得
,可得![]()
∵平面![]()
![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴平面![]() 的一个法向量是
的一个法向量是![]() ,
,
∴ ,即二面角
,即二面角![]() 的余弦值是
的余弦值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富高学生的课外生活,某校要组建数学计算机航空模型3个兴趣小组,小明要选报其中的2个,则包含的样本点共有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行
 天试销,每种单价试销
天试销,每种单价试销 天,得到如下数据:
天,得到如下数据:单价
 (元)
(元)




销量
 (册)
(册)




(1)求试销
 天的销量的方差和
天的销量的方差和 对
对 的回归直线方程;
的回归直线方程;(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是
 元,
元,为了获得最大利润,该单元卷的单价应定为多少元?
附:
 ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C. 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这个两个平面平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分,规定满意度不低于98分,则评价该教师为“优秀”,现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶);
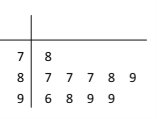
(1)指出这组数据的众数和中位数;
(2)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记
 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求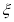 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在
 的频率及全班人数;
的频率及全班人数;(2)求分数在
 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中 间矩形的高;
间矩形的高;(3)若要从分数在
 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在 之间的概率.
之间的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中, 分别是
分别是 ,
, 上的点,
上的点, ,
, 是
是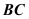 的中点,
的中点,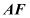 与
与 交于点
交于点 ,
, 沿
沿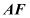 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥 ,其中
,其中 .
.
(1)求证:平面
 平面
平面
(2)若
 为
为 ,
, 上的中点,
上的中点,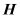 为
为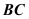 中点,求异面直线
中点,求异面直线 与
与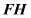 所成角的余弦值
所成角的余弦值
相关试题

