【题目】某游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为![]() ,奖励规则如下:①若
,奖励规则如下:①若![]() ,则奖励玩具一个;②若
,则奖励玩具一个;②若![]() ,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
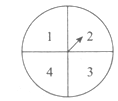
(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
参考答案:
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)由几何概型得到所有可能的事件,据此可得小亮获得玩具的概率是![]() ;
;
(2)结合古典概型计算公式可得小亮获得水杯与获得饮料的概率的大小,则小亮获得水杯的概率大于获得饮料的概率.
试题解析:
用数对![]() 表示小亮参加活动记录的数,则基本事件空间
表示小亮参加活动记录的数,则基本事件空间![]() 与点集
与点集![]() 一一对应,因为
一一对应,因为![]() 中元素个数是
中元素个数是![]() ,所以基本事件总数为
,所以基本事件总数为![]() .
.
(1)记“![]() ”为事件
”为事件![]() ,则事件
,则事件![]() 包含的基本事件共有
包含的基本事件共有![]() 个,即
个,即![]() .所以
.所以![]() ,即小亮获得玩具的概率为
,即小亮获得玩具的概率为![]() .
.
(2)即“![]() ”为事件
”为事件![]() ,“
,“![]() ”为事件
”为事件![]() ,则事件
,则事件![]() 包含的基本事件有
包含的基本事件有![]() 个,即
个,即![]() ,所以
,所以![]() ,则事件
,则事件![]() 包含的基本事件有
包含的基本事件有![]() 个,即
个,即![]() ,所以
,所以![]() ,所以小亮获得水杯的概率大于获得饮料的概率.
,所以小亮获得水杯的概率大于获得饮料的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
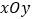 中,曲线
中,曲线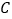 :
: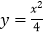 与直线
与直线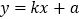 (
( )交于
)交于 ,
,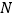 两点.
两点.(1)当
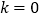 时,分别求
时,分别求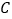 在点
在点 和
和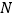 处的切线方程;
处的切线方程;(2)
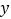 轴上是否存在点
轴上是否存在点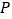 ,使得当
,使得当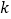 变动时,总有
变动时,总有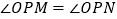 ?说明理由.
?说明理由. -
科目: 来源: 题型:
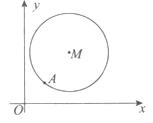
查看答案和解析>>【题目】如图,在平面直角坐标系
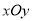 中,已知以
中,已知以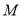 为圆心的圆
为圆心的圆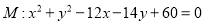 及其上一点
及其上一点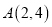 .
.
(1)是否存在直线
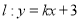 与圆
与圆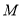 有两个交点
有两个交点 ,并且
,并且 ,若有,求此直线方程,若没有,请说明理由;
,若有,求此直线方程,若没有,请说明理由;(2)设点
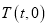 满足:存在圆
满足:存在圆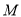 上的两点
上的两点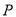 和
和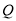 使得
使得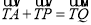 ,求实数
,求实数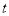 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均不相等的等差数列
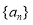 的前五项和
的前五项和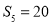 ,且
,且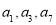 成等比数列.
成等比数列.(1)求数列
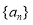 的通项公式;
的通项公式;(2)若
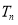 为数列
为数列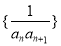 的前
的前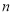 项和,且存在
项和,且存在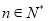 ,使得
,使得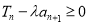 成立,求实数
成立,求实数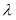 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
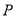 是椭圆
是椭圆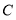 上任一点,点
上任一点,点 到直线
到直线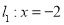 的距离为
的距离为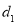 ,到点
,到点 的距离为
的距离为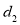 ,且
,且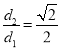 .直线
.直线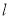 与椭圆
与椭圆 交于不同两点
交于不同两点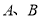 (
( 都在
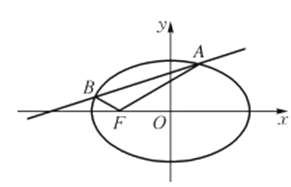
都在 轴上方),且
轴上方),且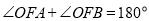 .
.
(1)求椭圆
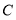 的方程;
的方程;(2)当
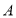 为椭圆与
为椭圆与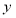 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线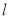 方程;
方程;(3)对于动直线
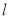 ,是否存在一个定点,无论
,是否存在一个定点,无论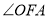 如何变化,直线
如何变化,直线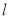 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
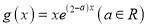 ,
, 为自然对数的底数.
为自然对数的底数.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)若函数
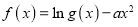 的图象与直线
的图象与直线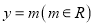 交于
交于 两点,线段
两点,线段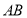 中点的横坐标为
中点的横坐标为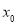 ,证明:
,证明: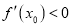 (
(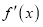 为函数
为函数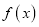 的导函数)
的导函数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
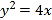 ,
,  是焦点,直线
是焦点,直线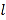 是经过点
是经过点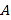 的任意直线.
的任意直线.(Ⅰ)若直线
 与抛物线交于
与抛物线交于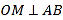 、
、 两点,且
两点,且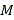 (
(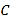 是坐标原点,
是坐标原点,  是垂足),求动点
是垂足),求动点 的轨迹方程;
的轨迹方程;(Ⅱ)若
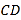 、
、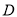 两点在抛物线
两点在抛物线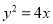 上,且满足
上,且满足 ,求证:直线
,求证:直线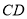 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
相关试题

