【题目】已知函数![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 的图象与直线
的图象与直线![]() 交于
交于![]() 两点,线段
两点,线段![]() 中点的横坐标为
中点的横坐标为![]() ,证明:
,证明:![]() (
(![]() 为函数
为函数![]() 的导函数)
的导函数)
参考答案:
【答案】(Ⅰ)详见解析; (Ⅱ)详见解析
【解析】
试题解析:(Ⅰ)由题可知,![]() 然后再,分
然后再,分![]() ,
,![]() ,
,![]() 三种情况,进行讨论,由此即可求出结果.(Ⅱ)化简可得
三种情况,进行讨论,由此即可求出结果.(Ⅱ)化简可得![]() ,可得
,可得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,与
上单调递增,与![]() 轴不可能有两个交点,故
轴不可能有两个交点,故![]() .当
.当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .故
.故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.不妨设
上单调递减.不妨设![]() ,且
,且![]() ,要证
,要证![]() ,需证
,需证![]() ,即证
,即证![]() ,又
,又![]() ,所以只需证
,所以只需证![]() .即证:当
.即证:当![]() 时,
时, ![]() .然后再构造辅助函数,再利用导数,即可证明结果.
.然后再构造辅助函数,再利用导数,即可证明结果.
试题解析:解:(1)由题可知,![]()
①当![]() 时,令
时,令![]() ,则
,则![]() ∴
∴![]()
令![]() ,则
,则![]() ∴
∴![]()
②当![]() 时,
时,![]()
③当![]() 时,令
时,令![]() ,则
,则![]() ∴
∴![]()
令![]() ,则
,则![]() ∴
∴![]()
综上:①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.当②
上单调递增.当②
![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
③当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)∵![]()
∴![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在
![]() 上单调递增,与
上单调递增,与![]() 轴不可能有两个交点,故
轴不可能有两个交点,故![]() .
.
当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .故
.故![]() 在
在![]() 上
上
单调递增,在![]() 上单调递减.不妨设
上单调递减.不妨设![]() ,且
,且![]() ,要证
,要证
![]() ,
,
需证![]() ,即证
,即证![]() ,
,
又![]() ,所以只需证
,所以只需证![]() .即证:当
.即证:当![]() 时,
时,
![]() .
.
设![]()
则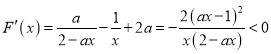 ,∴
,∴![]() 在
在![]() 上
上
单调递减,又![]() ,故
,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均不相等的等差数列
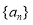 的前五项和
的前五项和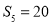 ,且
,且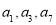 成等比数列.
成等比数列.(1)求数列
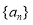 的通项公式;
的通项公式;(2)若
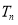 为数列
为数列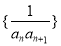 的前
的前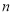 项和,且存在
项和,且存在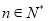 ,使得
,使得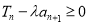 成立,求实数
成立,求实数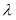 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为
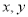 ,奖励规则如下:①若
,奖励规则如下:①若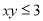 ,则奖励玩具一个;②若
,则奖励玩具一个;②若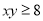 ,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.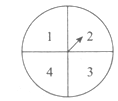
(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
-
科目: 来源: 题型:
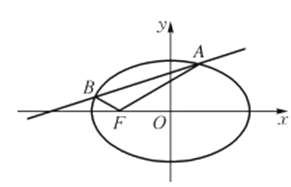
查看答案和解析>>【题目】已知点
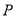 是椭圆
是椭圆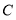 上任一点,点
上任一点,点 到直线
到直线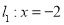 的距离为
的距离为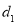 ,到点
,到点 的距离为
的距离为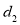 ,且
,且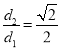 .直线
.直线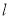 与椭圆
与椭圆 交于不同两点
交于不同两点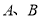 (
( 都在
都在 轴上方),且
轴上方),且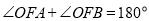 .
.
(1)求椭圆
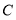 的方程;
的方程;(2)当
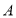 为椭圆与
为椭圆与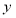 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线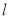 方程;
方程;(3)对于动直线
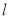 ,是否存在一个定点,无论
,是否存在一个定点,无论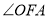 如何变化,直线
如何变化,直线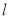 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
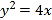 ,
,  是焦点,直线
是焦点,直线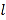 是经过点
是经过点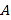 的任意直线.
的任意直线.(Ⅰ)若直线
 与抛物线交于
与抛物线交于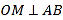 、
、 两点,且
两点,且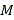 (
(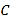 是坐标原点,
是坐标原点,  是垂足),求动点
是垂足),求动点 的轨迹方程;
的轨迹方程;(Ⅱ)若
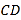 、
、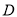 两点在抛物线
两点在抛物线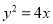 上,且满足
上,且满足 ,求证:直线
,求证:直线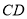 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府调查了工薪阶层
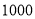 人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是
人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是 .(单位:百元)
.(单位:百元)
(1)为了了解工薪阶层对工资收人的满意程度,要用分层抽样的方法从调查的
 人中抽取
人中抽取 人做电话询问,求月工资收人在
人做电话询问,求月工资收人在 内应抽取的人数;
内应抽取的人数;(2)根据频率分布直方图估计这
 人的平均月工资为多少元.
人的平均月工资为多少元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
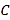 :
:  (
( )的两个焦点为
)的两个焦点为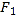 ,
, 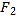 ,离心率为
,离心率为 ,点
,点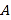 ,
, 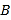 在椭圆上,
在椭圆上, 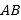 在线段
在线段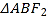 上,且
上,且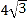 的周长等于
的周长等于 .
.(Ⅰ)求椭圆
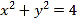 的标准方程;
的标准方程;(Ⅱ)过圆
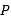 :
:  上任意一点
上任意一点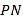 作椭圆
作椭圆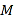 的两条切线
的两条切线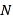 和
和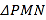 与圆
与圆 交于点
交于点 ,
, 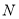 ,求
,求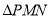 面积的最大值.
面积的最大值.
相关试题

