【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,
,![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由![]() 消参可得
消参可得![]() ,根据极坐标与普通方程的互化,
,根据极坐标与普通方程的互化,![]() ,
,![]() 代入化简得:
代入化简得:![]() ,故倾斜角为
,故倾斜角为![]() ;(2)点
;(2)点![]() 在直线
在直线![]() 上,可设直线
上,可设直线![]() 的参数方程为
的参数方程为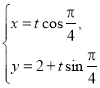 (
(![]() 为参数)代入椭圆方程化简得:
为参数)代入椭圆方程化简得:![]() ,则
,则![]() ,
,![]() ,又
,又![]() 故
故![]() .
.
试题解析:(1)由![]() 消去参数
消去参数![]() ,得
,得![]() ,
,
即![]() 的普通方程为
的普通方程为![]() .
.
由![]() ,得
,得![]() ,
,
将![]() 代入(*),化简得
代入(*),化简得![]() ,
,
所以直线![]() 的倾斜角为
的倾斜角为![]() .
.
(2)由(1)知,点![]() 在直线
在直线![]() 上,可设直线
上,可设直线![]() 的参数方程为
的参数方程为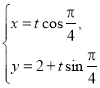 (
(![]() 为参数),即
为参数),即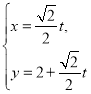 (
(![]() 为参数),
为参数),
代入![]() 并化简,得
并化简,得![]() .
.
![]() .设
.设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,
则![]() ,
,
所以![]() 所以
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
资金
每台产品所需资金(百元)
月资金供应量
(百元)
空调机
洗衣机
成本
30
20
300
劳动力(工资)
5
10
110
每台产品利润
6
8
试问:怎样确定两种货物的月供应量,才能使总利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
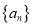 的奇数项是公差为
的奇数项是公差为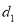 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为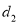 的等差数列,
的等差数列, 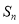 是数列
是数列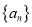 的前
的前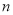 项和,
项和, 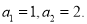
(1)若
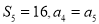 ,求
,求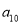 ;
;(2)已知
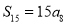 ,且对任意的
,且对任意的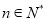 ,有
,有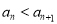 恒成立,求证:数列
恒成立,求证:数列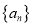 是等差数列;
是等差数列;(3)若
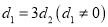 ,且存在正整数
,且存在正整数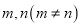 ,使得
,使得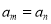 ,求当
,求当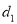 最大时,数列
最大时,数列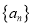 的通项公式.
的通项公式. -
科目: 来源: 题型:
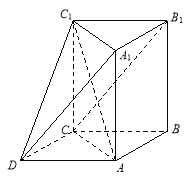
查看答案和解析>>【题目】如图所示的几何体中,
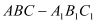 为三棱柱,且
为三棱柱,且 平面
平面 ,四边形
,四边形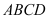 为平行四边形,
为平行四边形,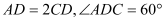 .
.
(1)若
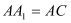 ,求证:
,求证: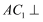 平面
平面 ;
;(2)若
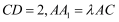 ,二面角
,二面角 的余弦值为
的余弦值为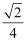 ,求三棱锥
,求三棱锥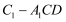 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
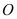 是坐标原点,若椭圆
是坐标原点,若椭圆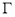 :
: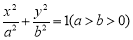 的离心率为
的离心率为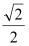 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为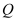 ,
,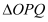 的面积为
的面积为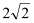 .
.(1)求椭圆
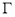 的标准方程;
的标准方程;(2)已知点
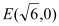 ,
,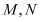 为椭圆
为椭圆 上两动点,若有
上两动点,若有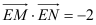 ,证明:直线
,证明:直线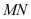 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用
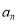 的信息如下图.
的信息如下图.
(1)求
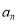 ;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
相关试题

