【题目】已知数列![]() 的奇数项是公差为
的奇数项是公差为![]() 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为![]() 的等差数列,
的等差数列, ![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和, ![]()
(1)若![]() ,求
,求![]() ;
;
(2)已知![]() ,且对任意的
,且对任意的![]() ,有
,有![]() 恒成立,求证:数列
恒成立,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() ,求当
,求当![]() 最大时,数列
最大时,数列![]() 的通项公式.
的通项公式.
参考答案:
【答案】(1)14;(2)证明见解析;(3) 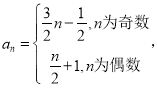
【解析】试题分析:
(1)利用题意求得公差,据此可得a10=14;
(2)结合(1)的结论证得d1=d2=2即可说明数列{an}是等差数列;
(3)分类讨论n的奇偶性即可得到数列的通项公式为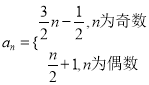 .
.
试题解析:
(1)根据题意,有a1=1,a2=2,a3=a1+d1=1+d1,a4=a2+d2=2+d2,a5=a3+d1=1+2d1∵S5=16,a4=a5
∴a1+a2+a3+a4+a5=7+3d1+d2=16,2+d2=1+2d1∴d1=2, d2=3.
∴a10=2+4d2=14
(2)证明:当n为偶数时,∵an<an+1恒成立,∴![]() ,
,
∴![]()
∴![]() 且d2>1
且d2>1
当n为奇数时,∵an<an+1恒成立,∴![]() ,
,
∴(1n)(d1d2)+2>0
∴![]()
∴d1=d2
∵S15=15a8,∴![]()
∴d1=d2=2
∴an=n
∴数列{an}是等差数列;
(3)若d1=3d2(d1≠0),且存在正整数m、n(m≠n),使得am=an,在m,n中必然一个是奇数,一个是偶数
不妨设m为奇数,n为偶数
∵am=an,∴![]()
∵d1=3d2,∴![]()
∵m为奇数,n为偶数,∴3mn1的最小正值为2,此时d1=3,d2=1
∴数列![]() 的通项公式为
的通项公式为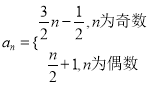 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为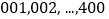 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为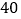 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为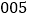 ,已知这
,已知这 名学生分住在三个营区,从
名学生分住在三个营区,从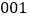 到
到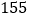 在第一营区,从
在第一营区,从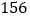 到
到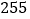 在第二营区,从
在第二营区,从 到
到 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
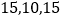 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
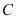 的方程:
的方程: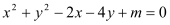
(1)求m的取值范围;
(2)若圆C与直线
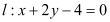 相交于
相交于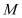 ,
,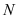 两点,且
两点,且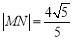 ,求
,求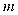 的值
的值(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
资金
每台产品所需资金(百元)
月资金供应量
(百元)
空调机
洗衣机
成本
30
20
300
劳动力(工资)
5
10
110
每台产品利润
6
8
试问:怎样确定两种货物的月供应量,才能使总利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,
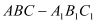 为三棱柱,且
为三棱柱,且 平面
平面 ,四边形
,四边形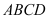 为平行四边形,
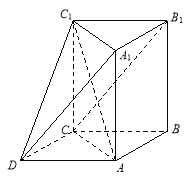
为平行四边形,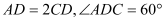 .
.
(1)若
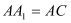 ,求证:
,求证: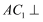 平面
平面 ;
;(2)若
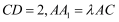 ,二面角
,二面角 的余弦值为
的余弦值为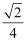 ,求三棱锥
,求三棱锥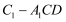 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修
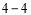 :坐标系与参数方程
:坐标系与参数方程在平面直角坐标系
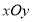 中,曲线
中,曲线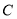 的参数方程为
的参数方程为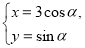 (
(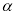 为参数),在以原点为极点,
为参数),在以原点为极点,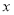 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线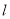 的极坐标方程为
的极坐标方程为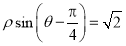 .
. (1)求
 的普通方程和
的普通方程和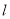 的倾斜角;
的倾斜角;(2)设点
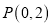 ,
,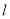 和
和 交于
交于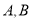 两点,求
两点,求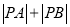 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
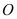 是坐标原点,若椭圆
是坐标原点,若椭圆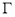 :
: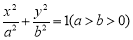 的离心率为
的离心率为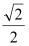 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为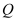 ,
,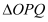 的面积为
的面积为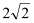 .
.(1)求椭圆
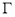 的标准方程;
的标准方程;(2)已知点
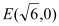 ,
,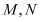 为椭圆
为椭圆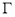 上两动点,若有
上两动点,若有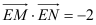 ,证明:直线
,证明:直线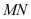 恒过定点.
恒过定点.
相关试题

