【题目】已知实数![]() 满足约束条件:
满足约束条件: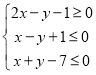 .
.
(1)请画出可行域,并求![]() 的最小值;
的最小值;
(2)若![]() 取最大值的最优解有无穷多个,求实数
取最大值的最优解有无穷多个,求实数![]() 的值.
的值.
参考答案:
【答案】(1)可行域见解析,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先根据约束条件画出可行域,![]() ,利用
,利用![]() 的几何意义求最值,只需求出何时可行域内的点与点
的几何意义求最值,只需求出何时可行域内的点与点![]() 连线的斜率的值最小,从而得到
连线的斜率的值最小,从而得到![]() 的最小值;(2)先根据约束条件画出可行域,设
的最小值;(2)先根据约束条件画出可行域,设![]() ,再利用
,再利用![]() 的几何意义求最值,只需求出直线
的几何意义求最值,只需求出直线![]() 与可行域的边界
与可行域的边界![]() 平行时,最优解有无穷多个,从而得到
平行时,最优解有无穷多个,从而得到![]() 值即可.
值即可.
试题解析:解:(1)如图求画出可行域:................. 2分
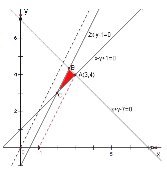
∵![]() 表示
表示![]() 与
与![]() 连线的斜率,如图示,
连线的斜率,如图示,
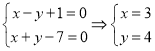 ,即
,即![]() ,
,
∴当![]() 时,
时,![]() ......................6分
......................6分
(2)取![]() 得直线
得直线![]() ,
,
∵当![]() 取得最值的最优解有无穷多个时,直线
取得最值的最优解有无穷多个时,直线![]() 与可行域边界所在直线平行,如图所示,当
与可行域边界所在直线平行,如图所示,当![]() ,即
,即![]() 时,
时,![]() 取最小值的最优解有无穷多个,不合题意,.............. 8分
取最小值的最优解有无穷多个,不合题意,.............. 8分
当![]() ,即
,即![]() 时,
时,![]() 取最大值的最优解有无穷多个,符合题意...............10分
取最大值的最优解有无穷多个,符合题意...............10分
当![]() ,即
,即![]() 时,
时,![]() 取最大值的最优解有无穷多个,符合题意.
取最大值的最优解有无穷多个,符合题意.
综上得,![]() .......................12分
.......................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
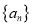 的前
的前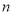 项和为
项和为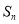 ,公差
,公差 ,且
,且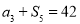 ,
,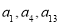 成等比数列.
成等比数列.(1)求数列
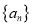 的通项公式;
的通项公式;(2)设
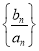 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列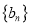 的前
的前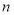 项和
项和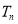 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
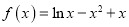 .
.(1)求函数
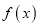 的单调区间;
的单调区间; (2)证明当
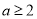 时,关于
时,关于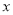 的不等式
的不等式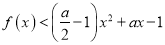 恒成立;
恒成立;(3)若正实数
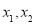 满足
满足 ,证明
,证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了
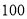 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间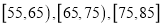 内的频率之比为
内的频率之比为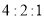 .
.(1) 求顾客年龄值落在区间
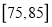 内的频率;
内的频率; (2) 拟利用分层抽样从年龄在
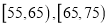 的顾客中选取
的顾客中选取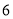 人召开一个座谈会,现从这
人召开一个座谈会,现从这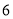 人中选出
人中选出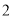 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.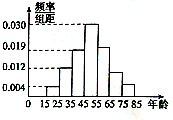
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获
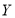 (单位:
(单位: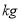 )与它的“相近”作物株数
)与它的“相近”作物株数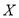 之间的关系如下表所示:
之间的关系如下表所示: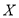
1
2
3
4
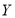
51
48
45
42
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
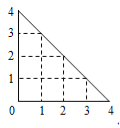
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定矩形春季校园足球联赛,为迎接此次联赛,甲同学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录如下表:
身高(
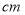 )
)168
174
175
176
178
182
185
188
人数
1
2
4
3
5
1
3
1
(1)请计算这20名学生的身高中位数、众数,并补充完成下面的茎叶图;

(2)身高为185
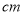 和188
和188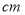 的四名学生分别为
的四名学生分别为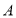 ,
,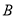 ,
,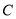 ,
,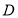 ,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生
,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生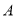 入选正门将的概率.
入选正门将的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
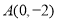 ,椭圆
,椭圆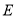 :
: 的离心率为
的离心率为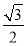 ,
,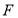 是椭圆
是椭圆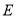 的右焦点,直线
的右焦点,直线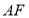 的斜率为
的斜率为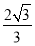 ,
, 为坐标原点.
为坐标原点.(1)求
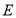 的方程;
的方程;(2)设过点
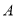 的动直线
的动直线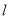 与
与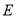 相交于
相交于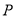 ,
,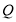 两点,当
两点,当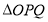 的面积最大时,求
的面积最大时,求 的直线方程.
的直线方程.
相关试题

