【题目】已知![]() ,
, ![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求动点![]() 的轨迹方程,并说明轨迹
的轨迹方程,并说明轨迹![]() 是什么图形;
是什么图形;
(2)求动点![]() 与定点
与定点![]() 连线的斜率的最小值;
连线的斜率的最小值;
(3)设直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,是否存在以线段
两点,是否存在以线段![]() 为直径的圆经过
为直径的圆经过![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() 轨迹
轨迹![]() 是以
是以![]() 为圆心,2为半径的圆;(2)
为圆心,2为半径的圆;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由直接法,设出点坐标列方程即可;
(2)由直线与圆有公共点可得![]() ,即可解得;
,即可解得;
(3)根据题意有![]() ,坐标化可得
,坐标化可得![]() ,进而直线和圆联立,由韦达定理代入求解即可.
,进而直线和圆联立,由韦达定理代入求解即可.
试题解析:
(1)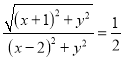 ,
,
化简可得: ![]() ,轨迹
,轨迹![]() 是以
是以![]() 为圆心,2为半径的圆
为圆心,2为半径的圆
(2)设过点![]() 的直线为
的直线为![]() ,圆心到直线的距离为
,圆心到直线的距离为![]()
∴![]() ,
, ![]()
(3)假设存在,联立方程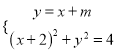 ,得
,得![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
![]() ,∴
,∴![]()
![]() ,得
,得![]() ,
,
![]() 且满足
且满足![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
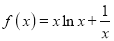 ,
,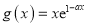 .
.(1) 求
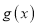 的单调区间;
的单调区间;(2) 若
 ,求满足
,求满足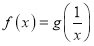 的实数
的实数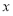 的取值集合.
的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水
 (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药 (单位:微克)的统计表:
(单位:微克)的统计表:
(1)令
 ,利用给出的参考数据求出
,利用给出的参考数据求出 关于
关于 的回归方程
的回归方程 .(
.( ,
, 精确到0.1)
精确到0.1)参考数据:
 ,
, ,
,
其中
 ,
,
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据
 )
)附:对于一组数据
 ,
, ,…,
,…, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
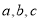 为三角形
为三角形 的三边,求证:
的三边,求证: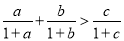
-
科目: 来源: 题型:
查看答案和解析>>【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为
 ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.(1)完成下面的
 列联表,并判断是否有
列联表,并判断是否有 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?比较关注
不太关注
合计
男生
女生
合计
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
 ,
, .
.
0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,且当x≥0时,
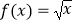 ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在
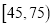 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差
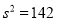 ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值 服从正态分布
服从正态分布 ,其中
,其中 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数 (注:求
(注:求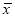 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表), 近似为样本方差
近似为样本方差 ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)(2)由以上统计数据完成下面
 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
附注:
参考数据:
 ,
,参考公式:
 ,
,  ,
,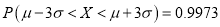 .
.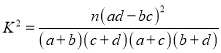

0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

