【题目】已知![]() ,
,![]() .
.
(1) 求![]() 的单调区间;
的单调区间;
(2) 若![]() ,求满足
,求满足![]() 的实数
的实数![]() 的取值集合.
的取值集合.
参考答案:
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(2)![]()
【解析】(1)由![]() 可得
可得![]() ,(1分)
,(1分)
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,令
时,令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(4分)
.(4分)
综上可得,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(5分)
.(5分)
(2)![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,
,
∴![]() 时
时![]() ,
,![]() 时
时![]() ,
,
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.(9分)
时取等号.(9分)
由(1)可知,当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
∴![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∴![]() 时,
时,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
即当且仅当![]() 时,
时,![]() ,
,
∴满足![]() 的实数
的实数![]() 的取值集合是
的取值集合是![]() .(12分)
.(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
,(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)讨论函数
 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占
 .现从参与者中随机选出200人,并将这200人按年龄分组:第
.现从参与者中随机选出200人,并将这200人按年龄分组:第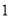 组
组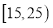 ,第
,第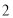 组
组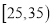 ,第
,第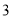 组
组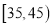 ,第
,第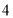 组
组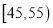 ,第
,第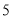 组
组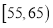 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有
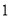 人年龄在第3组的概率;
人年龄在第3组的概率;(2)若从所有参与调查的人(人数很多)中任意选出3人,记关注民生问题的人数为X,求X的分布列与期望;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的人中老年人有10人,问是否有
 的把握认为是否关注民生问题与年龄有关?
的把握认为是否关注民生问题与年龄有关?附:
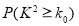
0.15
0.10
0.05
0.025
0.010
0.005
0.001
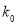
2.072
2.706
3.841
5.024
6.635
7.879
10.828
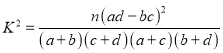 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为
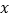 元/件(
元/件(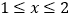 ),则新增的年销量
),则新增的年销量 (万件).
(万件).(1)写出今年商户甲的收益
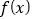 (单位:万元)与
(单位:万元)与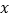 的函数关系式;
的函数关系式;(2)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水
 (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药 (单位:微克)的统计表:
(单位:微克)的统计表:
(1)令
 ,利用给出的参考数据求出
,利用给出的参考数据求出 关于
关于 的回归方程
的回归方程 .(
.( ,
, 精确到0.1)
精确到0.1)参考数据:
 ,
, ,
,
其中
 ,
,
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据
 )
)附:对于一组数据
 ,
, ,…,
,…, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
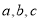 为三角形
为三角形 的三边,求证:
的三边,求证: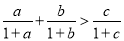
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
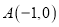 ,
, 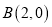 ,动点
,动点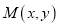 满足
满足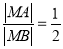 .设动点
.设动点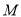 的轨迹为
的轨迹为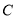 .
.(1)求动点
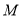 的轨迹方程,并说明轨迹
的轨迹方程,并说明轨迹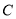 是什么图形;
是什么图形;(2)求动点
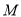 与定点
与定点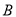 连线的斜率的最小值;
连线的斜率的最小值;(3)设直线
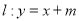 交轨迹
交轨迹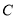 于
于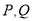 两点,是否存在以线段
两点,是否存在以线段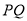 为直径的圆经过
为直径的圆经过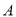 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
相关试题

