【题目】已知幂函数f(x)=x﹣m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)﹣ax+1,a为实常数,求g(x)在区间[﹣1,1]上的最小值.
参考答案:
【答案】解:(1)因为幂函数f(x)=x﹣m2+m+2 在(0,+∞)上单调递增,
所以﹣m2+m+2>0,故﹣1<m<2.
又因为m∈Z,故m=0,或m=1,所以f(x)=x2 .
(2)由(1)知g(x)=x2﹣ax+1,
①若![]() ≤﹣1,即a≤﹣2时,g(x)在[﹣1,1]上单调递增,
≤﹣1,即a≤﹣2时,g(x)在[﹣1,1]上单调递增,
所以g(x)mi n=g(﹣1)=a+2.
②若﹣1<![]() ≤1,即﹣2<a≤2时,
≤1,即﹣2<a≤2时,
g(x)在[﹣1,![]() ]上单调递减,[
]上单调递减,[![]() ,1]上单调递增,
,1]上单调递增,
所以g(x)min=g(\frac{a}{2})=1﹣![]() .
.
③若![]() >1,即a>2时,g(x)在[﹣1,1]上单调递减,
>1,即a>2时,g(x)在[﹣1,1]上单调递减,
所以g(x)min=g(1)=2﹣a.
综上:a≤﹣2时,g(x)在区间[﹣1,1]上的最小值为a+2;
﹣2<a≤2时,g(x)在区间[﹣1,1]上的最小值为1﹣![]() ;
;
a>2时,g(x)在区间[﹣1,1]上的最小值为2﹣a.
【解析】(1)由条件可得﹣m2+m+2>0,解得m的范围m.再结合m∈Z,求得m的值,可得f(x)的解析式.
(2)由(1)知g(x)=x2﹣ax+1,再分①若![]() ≤﹣1、②若﹣1<
≤﹣1、②若﹣1<![]() ≤1、③若
≤1、③若![]() >1三种情况,分别利用二次函数的性质,求得g(x)min . .
>1三种情况,分别利用二次函数的性质,求得g(x)min . .
【考点精析】解答此题的关键在于理解二次函数在闭区间上的最值的相关知识,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续
 天监测空气质量指数(
天监测空气质量指数(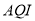 ),数据统计如下:
),数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出
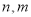 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;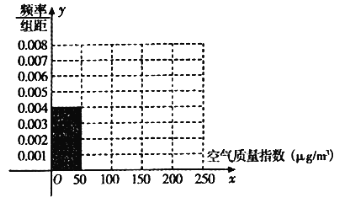
(2)由频率分布直方图求该组数据的平均数与中位数;
(3)在空气质量指数分别属于
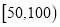 和
和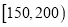 的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件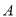 “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.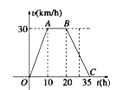
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.已知函数f(x)=1+a
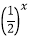 +
+ , g(x)=
, g(x)=
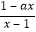 .
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[ , 3]上的所有上界构成的集合;
, 3]上的所有上界构成的集合;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.y=﹣x3
B.y=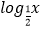
C.y=x
D.y=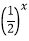
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差大于零的等差数列
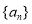 的前
的前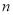 项和为
项和为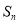 ,且
,且 ,
,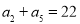 .
.(1)求数列
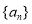 的通项公式;
的通项公式;(2)若数列
 是等差数列,且
是等差数列,且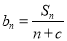 ,求非零常数
,求非零常数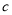 的值.
的值.(3)设
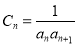 ,
,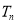 为数列
为数列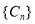 的前
的前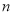 项和,是否存在正整数
项和,是否存在正整数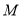 ,使得
,使得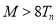 对任意的
对任意的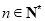 均成立?若存在,求出
均成立?若存在,求出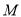 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
相关试题

