【题目】全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:

(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
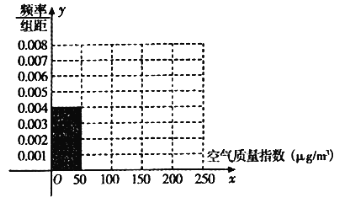
(2)由频率分布直方图求该组数据的平均数与中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
参考答案:
【答案】(1)![]() ,直方图见解析;(2)平均数为95,中位数为87.5;(3)
,直方图见解析;(2)平均数为95,中位数为87.5;(3)![]() .
.
【解析】试题分析:
(1)由题意可得![]() ,然后绘制直方图即可;
,然后绘制直方图即可;
(2)由正方体可知:平均数为95,中位数为87.5;
(3)利用概率知识结合古典概型公式求得事件![]() “两天空气都为良”发生的概率为
“两天空气都为良”发生的概率为![]()
试题解析:
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
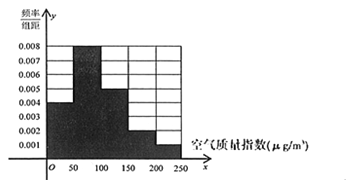
平均数为95,中位数为87.5;
在空气质量指数为![]() 的监测天数中分别抽取4天和1天,在所抽取
的监测天数中分别抽取4天和1天,在所抽取
的5天中,将空气质量指数为![]() 的4天分别记为
的4天分别记为![]() ;将空气质量指数
;将空气质量指数
为![]() 的1天分别记为
的1天分别记为![]() ;从中任取2天的基本事件分别为:
;从中任取2天的基本事件分别为:
![]() 共10种
共10种
其中事件A“两天空气都为良”包含的基本事件为:
![]() 共6种。
共6种。
所以事件A“两天空气都为良”发生的概率是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
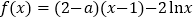 (
(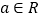 ).
).(Ⅰ)若曲线
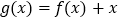 上点
上点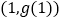 处的切线过点
处的切线过点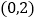 ,求函数
,求函数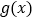 的单调减区间;
的单调减区间;(Ⅱ)若函数
 在
在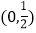 上无零点,求
上无零点,求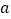 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为(结果保留一位小数.参考数据:
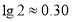 ,
,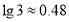 )
)A.1.3日 B.1.5日
C.2.6日 D.2.8日
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.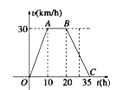
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=x﹣m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)﹣ax+1,a为实常数,求g(x)在区间[﹣1,1]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.已知函数f(x)=1+a
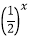 +
+ , g(x)=
, g(x)=
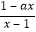 .
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[ , 3]上的所有上界构成的集合;
, 3]上的所有上界构成的集合;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
相关试题

