【题目】已知直线![]() 过坐标原点
过坐标原点![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
(1)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 与圆
与圆![]() 相交所得的弦长;
相交所得的弦长;
(2)设直线![]() 与圆
与圆![]() 交于两点
交于两点![]() ,且
,且![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) ![]() ;(2) 直线l的方程为y=x或y=﹣x.
;(2) 直线l的方程为y=x或y=﹣x.
【解析】试题分析:(1) 由已知,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 圆心为
圆心为![]() ,半径为
,半径为![]() ,求出圆心到直线
,求出圆心到直线![]() 的距离,根据勾股定理可求
的距离,根据勾股定理可求![]() 与圆
与圆![]() 相交所得的弦长;(2)设直线
相交所得的弦长;(2)设直线![]() 与圆
与圆![]() 交于两点
交于两点![]() ,且
,且![]() 为
为![]() 的中点,设
的中点,设![]()
![]() ,则
,则![]() ,将
,将![]() 点的坐标代入椭圆方程求出
点的坐标代入椭圆方程求出![]() 的坐标,即可求直线
的坐标,即可求直线![]() 的方程.
的方程.
试题解析:(1)由已知,直线l的方程为y=![]() x,圆C圆心为(0,3),半径为
x,圆C圆心为(0,3),半径为![]() ,
,
所以,圆心到直线l的距离为![]() =
=![]() .…
.…
所以,所求弦长为2![]() =2
=2![]() .
.
(2) 设A(x1,y1),因为A为OB的中点,则B(2x1,2y1).
又A,B在圆C上,
所以 x12+y12﹣6y1+4=0,4x12+4y12﹣12y1+4=0.
解得y1=1,x1=±1,
即A(1,1)或A(﹣1,1)
所以,直线l的方程为y=x或y=﹣x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex﹣ax,a是常数.
(Ⅰ)若a=1,且曲线y=f(x)的切线l经过坐标原点(0,0),求该切线的方程;
(Ⅱ)讨论f(x)的零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,设命题
,设命题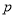 :指数函数
:指数函数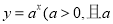 ≠
≠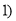 在
在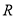 上单调递增.命题
上单调递增.命题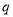 :函数
:函数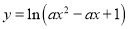 的定义域为
的定义域为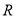 .若“
.若“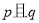 ”为假,“
”为假,“ ”为真,求
”为真,求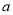 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.

(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆E:
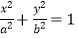 (a>b>0)的左右焦点分别为F1、F2 , D为椭圆短轴上的一个顶点,DF1的延长线与椭圆相交于G.△DGF2的周长为8,|DF1|=3|GF1|.
(a>b>0)的左右焦点分别为F1、F2 , D为椭圆短轴上的一个顶点,DF1的延长线与椭圆相交于G.△DGF2的周长为8,|DF1|=3|GF1|.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过椭圆E的左顶点A作椭圆E的两条互相垂直的弦AB、AC,试问直线BC是否恒过定点?若是,求出此定点的坐标;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为梯形,
为梯形,  底面
底面 ,
,  .过
.过 作一个平面
作一个平面 使得
使得 平面
平面 .
.(1)求平面
 将四棱锥
将四棱锥 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;(2)若平面
 与平面
与平面 之间的距离为
之间的距离为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

