【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 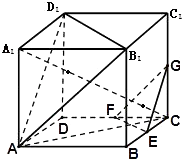
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG.
参考答案:
【答案】
(1)解:∵A1C∩平面ABCD=C,在正方体ABCD﹣A1B1C1D1中A1A⊥平面ABCD
∴AC为A1C在平面ABCD的射影
∴∠A1CA为A1C与平面ABCD所成角 ![]() 正方体的棱长为a∴AC=
正方体的棱长为a∴AC= ![]() a,A1C=
a,A1C= ![]() a
a
(2)证明:在正方体ABCD﹣A1B1C1D1中
连接BD,则DD1∥BB1,DD1=BB1,
∴D1DBB1为平行四边形
∴D1B1∥DB
∵E,F分别为BC,CD的中点
∴EF∥BD∴EF∥D1B1
∵EF平面GEF,D1B1平面GEF
∴D1B1∥平面GEF
同理AB1∥平面GEF
∵D1B1∩AB1=B1
∴平面AB1D1∥平面EFG.
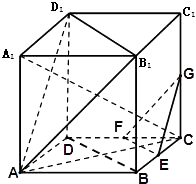
【解析】(1)欲求直线 A1C与平面ABCD所成角的正弦的值,在正方体ABCD﹣A1B1C1D1中,由于AC为A1C在平面ABCD的射影,故∠A1CA为A1C与平面ABCD所成角,最后在直角三角形中求解即得;(2)欲证平面AB1D1∥平面EFG,根据面面平行的判定定理可知,只须证明线面平行即可.在正方体ABCD﹣A1B1C1D1中连接BD,则DD1∥BB1 , DD1=BB1 , 利用直线间的平行关系可证得:D1B1∥平面GEF及AB1∥平面GEF,从而问题解决.
【考点精析】解答此题的关键在于理解平面与平面平行的判定的相关知识,掌握判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
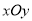 中,曲线
中,曲线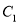 :
: 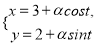 (
(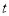 为参数,
为参数, 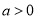 ),在以坐标原点为极点,
),在以坐标原点为极点, 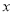 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线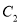 :
: 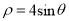 .
.(1)试将曲线
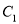 与
与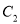 化为直角坐标系
化为直角坐标系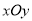 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时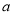 的取值范围;
的取值范围;(2)当
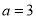 时,两曲线相交于
时,两曲线相交于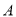 ,
, 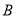 两点,求
两点,求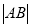 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)试讨论函数
 的单调性;
的单调性;(2)如果
 且关于
且关于 的方程
的方程 有两解
有两解 ,
,  (
( ),证明
),证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C为三角形ABC的三内角,其对应边分别为a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;
(2)若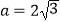 ,b+c=4,求三角形ABC的面积.
,b+c=4,求三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( )

A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24 -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
n
0.350
第3组
[170,175)
30
p
第4组
[175,180)
20
0.200
第5组
[180,185]
10
0.100
合计
100
1.000
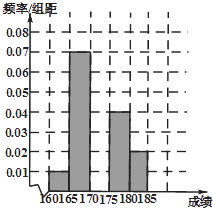
(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )
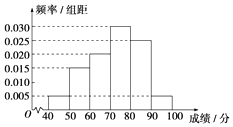
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
相关试题

