【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | n | 0.350 |
第3组 | [170,175) | 30 | p |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185] | 10 | 0.100 |
合计 | 100 | 1.000 |
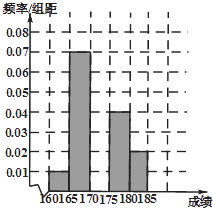
(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
参考答案:
【答案】
(1)解:由题意可知,第2组的频数n=0.35×100=35人,
第3组的频率p= ![]() ,
,
(2)解:∵第3、4、5组共有60名学生,
∴利用分层抽样在60名学生中抽取6名学生,
每组分别为:第3组: ![]() ×6=3人,第4组:
×6=3人,第4组: ![]() ×6=2人,第5组:
×6=2人,第5组: ![]() =1人,
=1人,
∴第3、4、5组分别抽取3人、2人、1人
(3)解:试验发生包含的事件是从六位同学中抽两位同学有C62=15种
满足条件的事件是第4组至少有一名学生被考官A面试有C21C41+1=9种结果,
∴至少有一位同学入选的概率为 ![]() =
= ![]()
【解析】(1)根据所给的第二组的频率,利用频率乘以样本容量,得到要求的频数,再根据所给的频数,利用频除以样本容量,得到要求的频率.(2)因为在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生,而这三个小组共有60人,利用每一个小组在60人中所占的比例,乘以要抽取的人数,得到结果.(3)试验发生包含的事件是从六位同学中抽两位同学有C62种满足条件的事件是第4组至少有一名学生被考官A面试有C21C41+1种结果,根据古典概型概率公式得到结果.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C为三角形ABC的三内角,其对应边分别为a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;
(2)若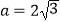 ,b+c=4,求三角形ABC的面积.
,b+c=4,求三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点.
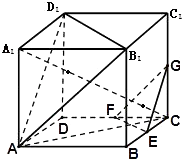
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( )

A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )
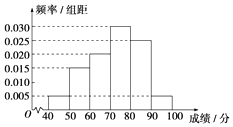
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为
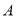 、
、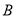 、
、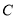 、
、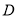 、
、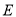 五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题: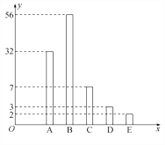
(1)试估算该校高三年级学生获得成绩为
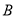 的人数;
的人数;(2)若等级
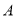 、
、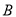 、
、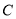 、
、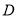 、
、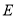 分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?(3)以每个学生的心理都培养成为健康状态为目标,学校决定对成绩等级为
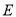 的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率.. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体
 中,四边形
中,四边形 为菱形,
为菱形,  ,
,  ,
,  ,
, 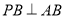 ,平面
,平面 平面
平面 ,
,  ,
,  为
为 的中点,
的中点,  为平面
为平面 内任一点.
内任一点.(1)在平面
 内,过
内,过 点是否存在直线
点是否存在直线 使
使 ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;(2)过
 ,
,  ,
,  三点的平面将几何体
三点的平面将几何体 截去三棱锥
截去三棱锥 ,求剩余几何体
,求剩余几何体 的体积.
的体积.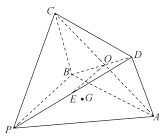
相关试题

