【题目】设函数![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)如果![]() 且关于
且关于![]() 的方程
的方程![]() 有两解
有两解![]() ,
, ![]() (
(![]() ),证明
),证明![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)求解函数的导函数,分类讨论可得:
①若![]() ,则当
,则当![]() 时,数
时,数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() 函数
函数![]() 单调递增;
单调递增;
②若![]() ,函数
,函数![]() 单调递增;
单调递增;
③若![]() ,则当
,则当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
(2)原问题即证明![]() ,构造新函数
,构造新函数![]()
![]() ,结合新函数的性质和题意即可证得结论.
,结合新函数的性质和题意即可证得结论.
试题解析:
(1)由![]() ,可知
,可知![]()
![]() .
.
因为函数![]() 的定义域为
的定义域为![]() ,所以,
,所以,
①若![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
②若![]() ,则当
,则当![]() 在
在![]() 内恒成立,函数
内恒成立,函数![]() 单调递增;
单调递增;
③若![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
(2)要证![]() ,只需证
,只需证![]() .
.
设![]()
![]() ,
,
因为![]() ,
,
所以![]() 为单调递增函数.
为单调递增函数.
所以只需证![]() ,
,
即证![]() ,
,
只需证![]()
![]() .(*)
.(*)
又![]() ,
, ![]() ,
,
所以两式相减,并整理,得![]()
![]() .
.
把![]()
![]() 代入(*)式,
代入(*)式,
得只需证![]() ,
,
可化为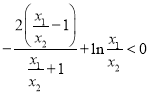 .
.
令![]() ,得只需证
,得只需证![]() .
.
令![]() (
(![]() ),
),
则![]()
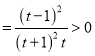 ,
,
所以![]() 在其定义域上为增函数,
在其定义域上为增函数,
所以![]() .
.
综上得原不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N,分别是AB,PC的中点;
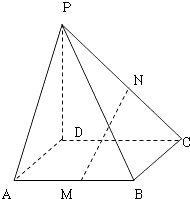
(1)求证:MN∥平面PAD;
(2)求四棱锥P﹣ABCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
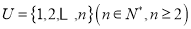 ,对于集合
,对于集合 的两个非空子集
的两个非空子集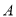 ,
, 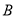 ,若
,若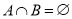 ,则称
,则称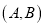 为集合
为集合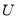 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为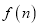 (视
(视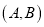 与
与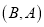 为同一组“互斥子集”).
为同一组“互斥子集”).(1)写出
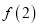 ,
,  ,
, 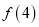 的值;
的值;(2)求
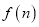 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
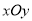 中,曲线
中,曲线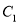 :
: 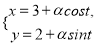 (
(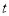 为参数,
为参数, 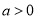 ),在以坐标原点为极点,
),在以坐标原点为极点, 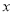 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线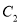 :
: 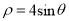 .
.(1)试将曲线
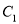 与
与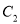 化为直角坐标系
化为直角坐标系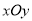 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时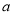 的取值范围;
的取值范围;(2)当
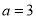 时,两曲线相交于
时,两曲线相交于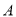 ,
, 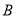 两点,求
两点,求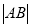 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C为三角形ABC的三内角,其对应边分别为a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;
(2)若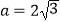 ,b+c=4,求三角形ABC的面积.
,b+c=4,求三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点.
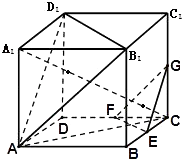
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( )

A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24
相关试题

