【题目】下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解
参考答案:
【答案】B
【解析】解:A、∵a=7,b=14,A=30°,
∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =1,
=1,
又B为三角形的内角,
∴B=90°,C=60°,c=7 ![]() ,
,
则此时三角形只有一解,此选项错误;
B、∵a=30,b=25,A=150°,
∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() ,
,
∵a>b,∴150°>A>B,
则此时B只有一解,本选项正确;
C、∵a=6,b=9,A=45°,
∴∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() >
> ![]() ,
,
∵b>a,∴B>A=45°,
∴此时B只有一解,本选项错误;
D、∵a=9,b=10,A=60°,
∴∴由正弦定理 ![]() =
= ![]() 得:sinB=
得:sinB= ![]() =
= ![]() >
> ![]() ,
,
∵a<b,∴60°=A<B,
此时B有两解,本选项错误,
故选B
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点C(t,
 )(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)当t=2时,求圆C的方程;
(2)求证:△OAB的面积为定值;
(3)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的离心率为
的离心率为 ,圆心在
,圆心在 轴的正半轴上的圆
轴的正半轴上的圆 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆 的半径为2,则以圆
的半径为2,则以圆 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )A.
 B.
B. 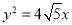 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=sin2(2x﹣
 )﹣2tsin(2x﹣
)﹣2tsin(2x﹣  )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ 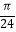 ,
,  ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
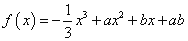 ,
, ,其中
,其中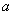 ,
, .
.
(Ⅰ)若函数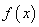 在
在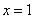 处有极小值
处有极小值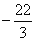 ,求
,求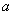 ,
,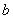 的值;
的值;
(Ⅱ)若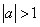 ,设
,设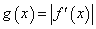 ,求证:当
,求证:当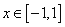 时,
时,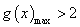 ;
;
(Ⅲ)若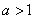 ,
,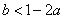 ,对于给定
,对于给定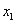 ,
, ,
, ,
,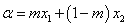 ,
,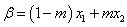 ,其中
,其中 ,
, ,
,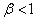 ,若
,若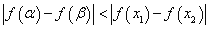 .求
.求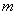 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
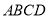 为菱形,
为菱形, 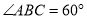 ,
, 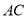 与
与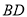 相交于点
相交于点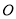 ,
, 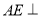 平面
平面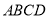 ,
, 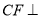 平面
平面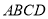 ,
, 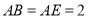 ,
, 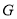 为
为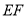 中点.
中点.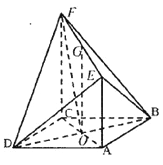
(Ⅰ)求证:
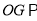 平面
平面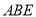 ;
;(Ⅱ)求二面角
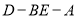 的正弦值;
的正弦值;(Ⅲ)当直线
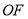 与平面
与平面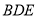 所成角为
所成角为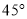 时,求异面直线
时,求异面直线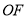 与
与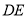 所成角的余弦值.
所成角的余弦值.
相关试题

