【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
参考答案:
【答案】
(1)解:∵x∈[ ![]() ,
, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴f(x)=[sin(2x﹣ ![]() ﹣t]2﹣6t+1,
﹣t]2﹣6t+1,
当t<﹣ ![]() 时,则当sinx=﹣
时,则当sinx=﹣ ![]() 时,f(x)min=
时,f(x)min= ![]() ;
;
当﹣ ![]() ≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
当t>1时,当sinx=1时,f(x)min=t2﹣8t+2;
∴g(t)= 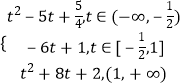
(2)解:当 ![]() 时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
欲使g(t)=kt有一个实根,则只需使 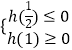 或
或 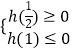 即可.
即可.
解得k≤﹣8或k≥﹣5.
【解析】(1)利用x的范围确定sin(2x﹣ ![]() ),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当
),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当 ![]() 时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣
时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣ ![]() )和h(1)异号即可.
)和h(1)异号即可.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设
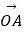 =
= 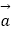 ,
, 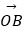 =
= 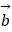 ,
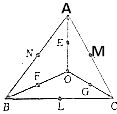
, 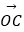 =
= 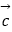 .
. 
(1)试用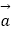 ,
, 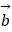 ,
, 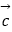 表示向量
表示向量 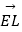 ,
, 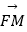 ,
, 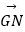 ;
;
(2)证明:线段EL,FM,GN交于一点且互相平分. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点C(t,
 )(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)当t=2时,求圆C的方程;
(2)求证:△OAB的面积为定值;
(3)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 的离心率为
的离心率为 ,圆心在
,圆心在 轴的正半轴上的圆
轴的正半轴上的圆 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆 的半径为2,则以圆
的半径为2,则以圆 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )A.
 B.
B. 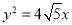 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
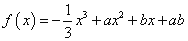 ,
, ,其中
,其中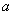 ,
, .
.
(Ⅰ)若函数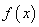 在
在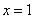 处有极小值
处有极小值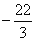 ,求
,求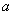 ,
,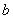 的值;
的值;
(Ⅱ)若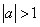 ,设
,设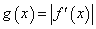 ,求证:当
,求证:当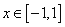 时,
时,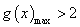 ;
;
(Ⅲ)若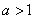 ,
,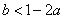 ,对于给定
,对于给定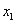 ,
, ,
, ,
,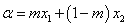 ,
,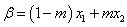 ,其中
,其中 ,
, ,
,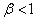 ,若
,若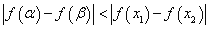 .求
.求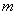 的取值范围.
的取值范围.
相关试题

