【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的最大值为
的最大值为![]() ;
;
②![]() 的最小正周期是
的最小正周期是![]() ;
;
③![]() 在区间
在区间![]() 上是减函数;
上是减函数;
④直线![]() 是函数
是函数![]() 的一条对称轴方程.
的一条对称轴方程.
其中正确结论的序号是__________.
参考答案:
【答案】②④
【解析】由题意得,f(x)=cos(2x![]() )+sin(2x+
)+sin(2x+![]() )=
)=![]() cos2x+
cos2x+![]() sin2x+
sin2x+![]() sin2x+
sin2x+![]() cos2x=
cos2x=![]() sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+![]() )
)
①、当sin(2x+![]() )=1时,y=f(x)取到最大值为2,①不正确;
)=1时,y=f(x)取到最大值为2,①不正确;
②、由T=![]() =π得,y=f(x)的最小正周期是π,②正确;
=π得,y=f(x)的最小正周期是π,②正确;
③、由x∈[![]() ]得,2x+
]得,2x+![]() ∈[0,
∈[0,![]() ],
],
所以y=f(x)在区间[![]() ]上不是单调函数,③不正确;
]上不是单调函数,③不正确;
④、当x=![]() 时,2x+
时,2x+![]() =
=![]() ,
,
所以直线x=![]() 是函数y=f(x)的一条对称轴方程,④正确,
是函数y=f(x)的一条对称轴方程,④正确,
故答案为:②④。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
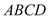 为矩形,直线
为矩形,直线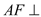 平面
平面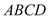 ,
,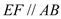 ,
,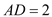 ,
, ,点
,点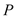 在棱
在棱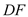 上.
上.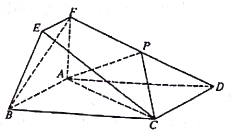
(1)求证:
 ;
;(2)若
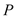 是
是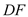 的中点,求异面直线
的中点,求异面直线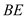 与
与 所成角的余弦值;
所成角的余弦值;(3)若


 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某件商品的经验表明,该商品每日的销量
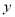 (单位:千克)与销售价格
(单位:千克)与销售价格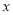 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式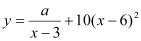 ,其中
,其中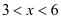 ,
,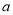 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。(Ⅰ)求实数
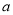 的值;
的值;(Ⅱ)若该商品的成本为3元/千克,试确定销售价格
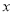 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛.图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照
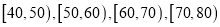 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.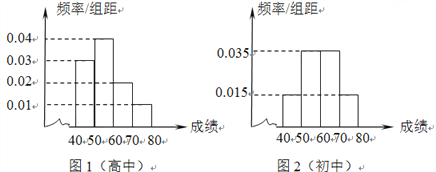
(1)分别计算参加这次知识竞赛的两个学段的学生的平均成绩;
(2)规定竞赛成绩达到
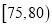 为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;(3)完成下列
 的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?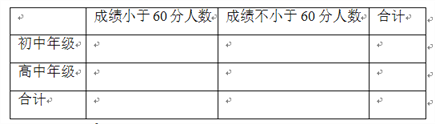
附:
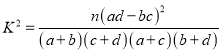
临界值表:
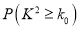
0.10
0.05
0.01
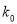
2.706
3.841
6.635
-
科目: 来源: 题型:
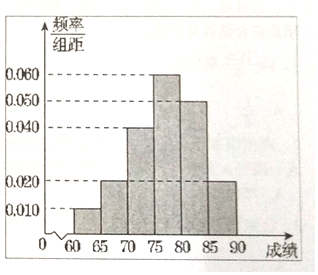
查看答案和解析>>【题目】在某次综合素质测试中,共设有60个考场,每个考场30名考生,在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考场中座位号为06的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
问:
在这个调查采样中,采用的是什么抽样方法?
估计这次测试中优秀(80分及以上)的人数;
写出这60名考生成绩的众数、中位数、平均数的估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
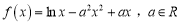 ,且
,且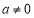 .
.(1)若函数
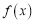 在区间
在区间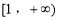 上是减函数,求实数
上是减函数,求实数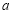 的取值范围;
的取值范围;(2)设函数
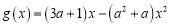 ,当
,当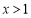 时,
时,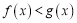 恒成立,求
恒成立,求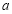 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
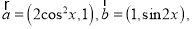 函数
函数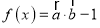
(1)
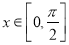 求函数
求函数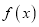 的值域;
的值域;(2)求方程
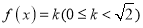 ,在
,在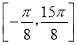 内的所有实数根之和.
内的所有实数根之和.
相关试题

