【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ,
, ![]() (2) 存在正整数
(2) 存在正整数![]()
【解析】试题分析:(1)代入![]() ,解得
,解得![]() ,根据周期定义可得
,根据周期定义可得![]() (2)先
(2)先![]() ,根据绝对值分两类:
,根据绝对值分两类: ![]() ,再根据同角关系转化为二次函数,根据二次方程解的情况讨论零点情况,最后根据
,再根据同角关系转化为二次函数,根据二次方程解的情况讨论零点情况,最后根据![]() 个数确定
个数确定![]() 的值
的值
试题解析:(1)![]() ,
, ![]()
(2)存在![]() ,满足题意
,满足题意
理由如下:
当![]() 时,
时, ![]()
![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
, ![]() 可得
可得![]() 或
或![]() ,由
,由![]()
图像可知, ![]() 在
在![]() 上有
上有![]() 个零点满足题意
个零点满足题意
当![]() 时,
时, ![]()
![]() ,
, ![]() ,则,
,则, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() 或
或![]() ,因为
,因为![]() ,
,
所以![]() 在
在![]() 上不存在零点。
上不存在零点。
综上讨论知:函数![]() 在
在![]() 上有
上有![]() 个零点,而
个零点,而![]() ,因此函数
,因此函数![]() 在有
在有![]() 个零点,所以存在正整数
个零点,所以存在正整数![]() 满足题意.
满足题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
 =1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且
=1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且  共线.
共线.
(1)求椭圆的离心率;
(2)当三角形AOB的面积S△AOB= 时,求椭圆的方程.
时,求椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据平面向量基本定理,若
 为一组基底,同一平面的向量
为一组基底,同一平面的向量 可以被唯一确定地表示为
可以被唯一确定地表示为  =
=  ,则向量
,则向量 与有序实数对
与有序实数对 一一对应,称
一一对应,称 为向量
为向量 的基底
的基底 下的坐标;特别地,若
下的坐标;特别地,若 分别为
分别为 轴正方向的单位向量
轴正方向的单位向量 ,则称
,则称 为向量
为向量 的直角坐标.
的直角坐标.(I)据此证明向量加法的直角坐标公式:若
 ,则
,则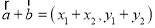 ;
;(II)如图,直角
 中,
中,  ,
,  点在
点在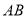 上,且
上,且 ,求向量
,求向量 在基底
在基底 下的坐标.
下的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn=
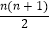 ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 的半径为2,圆心在
的半径为2,圆心在 轴的正半轴上,且与直线
轴的正半轴上,且与直线 相切.
相切.(1)求圆
 的方程。
的方程。(2)在圆
 上,是否存在点
上,是否存在点 ,使得直线
,使得直线 与圆
与圆 相交于不同的两点
相交于不同的两点 ,且△
,且△ 的面积最大?若存在,求出点
的面积最大?若存在,求出点 的坐标及对应的△
的坐标及对应的△ 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份
2010
2011
2012
2013
2014
2015
2016
年份代号x
1
2
3
4
5
6
7
人均纯收入y
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: =
=  ,
,  =
=  ﹣
﹣  .
.
相关试题

