【题目】如图,PA、PC切⊙O于A、C,PBD为⊙O的割线. 
(1)求证:ADBC=ABDC;
(2)已知PB=2,PA=3,求△ABC与△ACD的面积之比.
参考答案:
【答案】
(1)证明:∵PA是⊙O的切线,
由弦切角定理得∠PAB=∠ADB,
∵∠APB为△PAB与△PAD的公共角,
∴△PAB∽△PDA,
∴ ![]() ,
,
同理 ![]() ,
,
又PA=PC,
∴ ![]() ,
,
∴ADBC=ABDC
(2)解:由圆的内接四边形的性质得∠ABC+∠ADC=π,
∴S△ABC= ![]() ABBCsin∠ABC,
ABBCsin∠ABC,
S△ADC= ![]() ADDCsin∠ADC,
ADDCsin∠ADC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(1)证明△PAB∽△PDA,可得 ![]() ,同理可得
,同理可得 ![]() ,问题得以证明,(2)根据圆内接四边形的性质和三角形的面积公式可得
,问题得以证明,(2)根据圆内接四边形的性质和三角形的面积公式可得 ![]() =
= ![]() ,问题得以解决.
,问题得以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
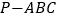 中,
中,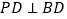 ,
,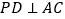 ,
,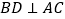 ,且
,且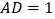 ,
,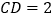 ,
,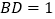 ,
,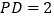 ,
,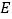 为
为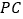 上一点,
上一点,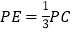 .
.(1)求证:
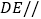 平面
平面 ;
;(2)求异面直线
 和
和 所成角的余弦值.
所成角的余弦值.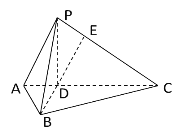
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种出口产品的关税税率
 ,市场价格
,市场价格 (单位:千元)与市场供应量
(单位:千元)与市场供应量 (单位:万件)之间近似满足关系式:
(单位:万件)之间近似满足关系式: ,其中
,其中 、
、 均为常数.当关税税率为
均为常数.当关税税率为 时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为
时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为 时,若市场价格为7千元,则市场供应量约为2万件.
时,若市场价格为7千元,则市场供应量约为2万件.(1)试确定
 、
、 的值;
的值;(2)市场需求量
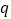 (单位:万件)与市场价格
(单位:万件)与市场价格 近似满足关系式:
近似满足关系式: .当
.当 时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
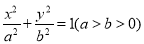 上的焦点为
上的焦点为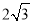 ,离心率为
,离心率为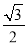 .
.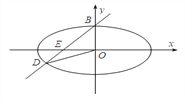
(1)求椭圆方程;
(2)设过椭圆顶点
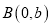 ,斜率为
,斜率为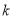 的直线交椭圆于另一点
的直线交椭圆于另一点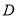 ,交
,交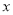 轴于点
轴于点 ,且
,且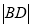 ,
,  ,
, 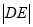 成等比数列,求
成等比数列,求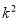 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,已知⊙O的方程x2+y2=4,直线l:x=4,在以O为极点,x轴的正半轴为极轴的极坐标系中,过极点作射线交⊙O于A,交直线l于B.
(1)写出⊙O及直线l的极坐标方程;
(2)设AB中点为M,求动点M的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的定义域为
的定义域为 ,若对于任意的
,若对于任意的 ,,当
,,当 时,都有
时,都有 ,则称函数
,则称函数 在
在 上为非减函数.设函数
上为非减函数.设函数 在
在 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③ ,则
,则 等于( ).
等于( ).A.
 B.
B.  C.
C.  D.
D. 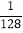
-
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (
 ,2] B. [
,2] B. [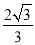 ,2) C. (
,2) C. (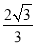 ,+
,+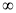 ) D. [
) D. [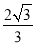 ,+
,+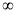 )
)
相关试题

