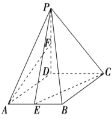
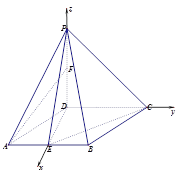
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)见解析.
(2) ![]() .
.
【解析】
试题分析:(1)作![]() 交
交![]() 于
于![]() 根据条件可证得
根据条件可证得![]() 为平行四边形,从而根据线面平行的判定,即可得证;(2)建立空间直角坐标系,根据条件中的数据可求得平面平面PAB的一个法向量为
为平行四边形,从而根据线面平行的判定,即可得证;(2)建立空间直角坐标系,根据条件中的数据可求得平面平面PAB的一个法向量为![]() ,从而问题可等价转化为求
,从而问题可等价转化为求![]() 与
与![]() 的夹角.
的夹角.
试题解析:(1)作![]() 交
交![]() 于
于![]() ,∵点
,∵点![]() 为
为![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ,∴
,∴![]() 为平行四边形,∴
为平行四边形,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;(2)∵
;(2)∵![]() ,∴
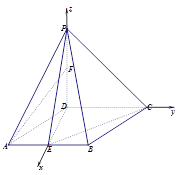
,∴![]() ,如图所示,建立坐标系,则
,如图所示,建立坐标系,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,∵
,∵![]() ,
,![]() ,∴
,∴ ,取
,取![]() ,则
,则![]() ,∴平面PAB的一个法向量为
,∴平面PAB的一个法向量为![]() ,∵
,∵![]() ,∴设向量
,∴设向量![]() 与
与![]() 所成角为
所成角为![]() ,
,
∴ ,∴
,∴![]() 平面
平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线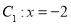 ,圆
,圆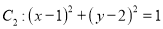 .以原点
.以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求
 的极坐标方程;
的极坐标方程;(2)若直线
 的极坐标方程为
的极坐标方程为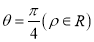 ,设
,设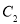 与
与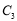 的交点为
的交点为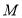 、
、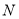 ,求
,求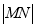 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:
 ,
, ,
, ,
, ,
, ,
, (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:
其中,屏幕需求尺寸在
 的一组人数为50人.
的一组人数为50人.(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为
 和
和 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在
 和
和 的概率是多少?
的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数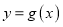 为函数
为函数 的反函数.
的反函数.(1)求函数
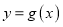 的解析式;
的解析式;(2)若方程
 恰有一个实根,求实数
恰有一个实根,求实数 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意 ,当
,当 时,满足
时,满足 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
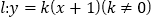 与椭圆
与椭圆 相交于
相交于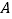 ,
,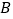 两个不同的点,与
两个不同的点,与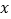 轴相交于点
轴相交于点 ,
,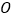 为坐标原点.
为坐标原点.(1)证明:
 ;
;(2)若
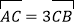 ,求
,求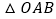 的面积取得最大值时椭圆的方程.
的面积取得最大值时椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
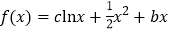
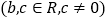 ,且
,且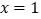 为
为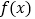 的极值点.
的极值点.(Ⅰ) 若
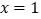 为
为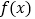 的极大值点,求
的极大值点,求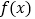 的单调区间(用
的单调区间(用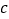 表示);
表示);(Ⅱ)若
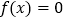 恰有1解,求实数
恰有1解,求实数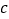 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
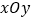 中,曲线
中,曲线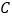 的参数方程为
的参数方程为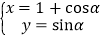 (
(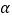 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,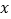 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线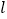 的极坐标方程为
的极坐标方程为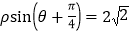 .
.(1)求曲线
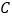 和直线
和直线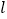 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;(2)动点
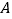 在曲线
在曲线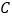 上,动点
上,动点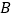 在直线
在直线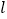 上,定点
上,定点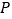 的坐标为
的坐标为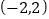 ,求
,求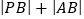 的最小值.
的最小值.
相关试题

