搜索
【题目】数列{an}满足a1=1，nan+1=（n+1）an+n（n+1），n∈N* ． （Ⅰ）证明：数列{ 
}是等差数列；
（Ⅱ）设bn=3n 
，求数列{bn}的前n项和Sn ．
参考答案：
【答案】证明（Ⅰ）∵nan+1=（n+1）an+n（n+1）， ∴ 
，
∴ 
，
∴数列{ 
}是以1为首项，以1为公差的等差数列；
（Ⅱ）由（Ⅰ）知， 
，
∴ 
，
bn=3n 
=n3n ，
∴ 
3n﹣1+n3n①
3n+n3n+1②
① ﹣②得 
3n﹣n3n+1
= 
= 
∴ 
【解析】（Ⅰ）将nan+1=（n+1）an+n（n+1）的两边同除以n（n+1）得 
，由等差数列的定义得证．（Ⅱ）由（Ⅰ）求出bn=3n 
=n3n ， 利用错位相减求出数列{bn}的前n项和Sn ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设△ABC的内角A，B，C所对的边分别为a，b，c且acosC﹣
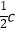=b．
（1）求角A的大小；
（2）若a=1，求△ABC的周长的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（第x周）和市场占有率（y﹪）的几组相关数据如下表：
1
2
3
4
5
0.03
0.06
0.1
0.14
0.17
（Ⅰ）根据表中的数据，用最小二乘法求出
关于
的线性回归方程
；（Ⅱ）根据上述线性回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测在第几周，该款旗舰机型市场占有率将首次超过 0.40﹪（最后结果精确到整数）.
参考公式：
，
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用（单位：元）,
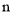表示购机的同时购买的易损零件数.（Ⅰ）若
=19,求y与x的函数解析式；（Ⅱ）若要求“需更换的易损零件数不大于
”的频率不小于0.5,求
的最小值；（Ⅲ）假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】2016年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速
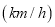分成六段：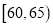 
， 
， 
， 
， 
， 
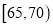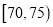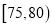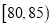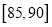后得到如图的频率分布直方图．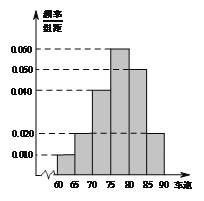
（I）某调查公司在采样中，用到的是什么抽样方法？
（II）求这40辆小型车辆车速的众数、中位数及平均数的估计值；
(III)若从车速在
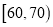的车辆中任抽取2辆，求车速在
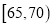的车辆至少有一辆的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】某食品厂定期购买面粉．已知该厂每天需用面粉6t，每吨面粉的价格为1800元，面粉的保管等其他费用为平均每吨每天3元，购面粉每次需支付运费900元．
（1）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
（2）若提供面粉的公司规定：当一次购买面粉不少于210t时，其价格可享受9折优惠（即原价的90%），问该厂是否考虑利用此优惠条件？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为
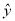＝0.85x－85.71，则下列结论中不正确的是( )A. y与x具有正的线性相关关系
B. 若给变量x一个值，由回归直线方程
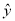＝0.85x－85.71得到一个
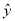，则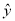
为该统计量中的估计值C. 若该大学某女生身高增加1 cm，则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg
相关试题
