【题目】某村计划建造一个室内面积为800m2的矩形蔬菜温室,在室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
参考答案:
【答案】长为20m,宽为40m.,最大种植面积为648.
【解析】试题分析:设出矩形的长为a与宽b,建立蔬菜面积关于矩形边长的函数关系式S=(a-4)(b-2)=ab-4b-2a+8=800-2(a+2b).利用基本不等式变形求解
试题解析:设矩形温室的左侧边长为a m,后侧边长为b m,则 ab=800.
蔬菜的种植面积![]()
所以![]()
当![]()
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
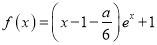 ,其中
,其中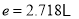 为自然对数的底数,常数
为自然对数的底数,常数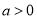 .
.(1)求函数
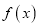 在区间
在区间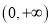 上的零点个数;
上的零点个数;(2)函数
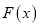 的导数
的导数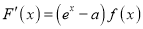 ,是否存在无数个
,是否存在无数个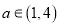 ,使得
,使得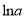 为函数
为函数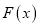 的极大值点?说明理由.
的极大值点?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
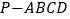 ,底面
,底面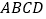 为菱形,
为菱形,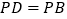 ,
,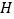 为
为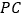 上的点,过
上的点,过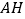 的平面分别交
的平面分别交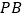 ,
, 于点
于点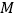 ,
,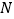 ,且
,且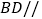 平面
平面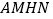 .
.(1)证明:
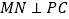 ;
;(2)当
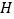 为
为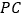 的中点,
的中点,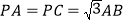 ,
,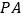 与平面
与平面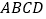 所成的角为
所成的角为 ,求二面角
,求二面角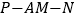 的余弦值.
的余弦值.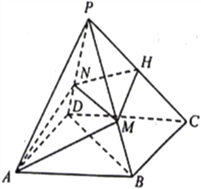
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
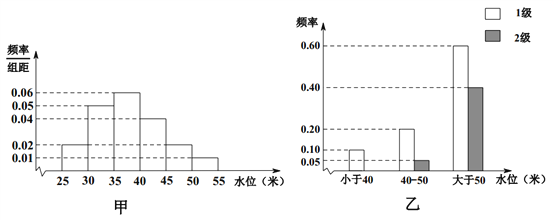
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案
防控等级
费用(单位:万元)
方案一
无措施
0
方案二
防控1级灾害
40
方案三
防控2级灾害
100
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】11月11日有2000名网购者在某购物网站进行网购消费(金额不超过1000元),其中女性1100名,男性900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析,如表.(消费金额单位:元)

(1)计算
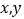 的值,在抽出的200名且消费金额在
的值,在抽出的200名且消费金额在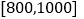 的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上数据列
 列联表,并回答能否有
列联表,并回答能否有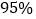 的把握认为“是否为网购达人与性别有关?”附:
的把握认为“是否为网购达人与性别有关?”附: ,
,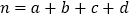

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
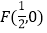 为抛物线
为抛物线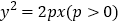 的焦点,点
的焦点,点 为其上一点,
为其上一点,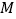 与
与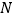 关于
关于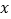 轴对称,直线
轴对称,直线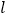 与抛物线交于异于
与抛物线交于异于 的
的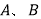 两点,
两点,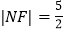 ,
,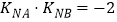 .
.(1)求抛物线的标准方程和
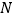 点的坐标;
点的坐标;(2)判断是否存在这样的直线
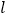 ,使得
,使得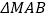 的面积最小.若存在,求出直线
的面积最小.若存在,求出直线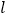 的方程和
的方程和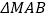 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
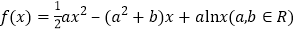 .
.(1)当
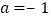 ,
,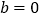 时,求函数
时,求函数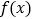 在
在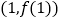 处的切线方程;
处的切线方程;(2)当
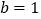 时,求函数
时,求函数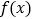 的单调区间;
的单调区间;(3)在(1)的条件下,证明:
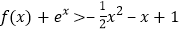 (其中
(其中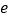 为自然对数的底数)
为自然对数的底数)
相关试题

