【题目】某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.

根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:K2=![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考答案:
【答案】列联表见解析,在犯错误的概率不超过![]() 的前提下认为:“成绩优秀”与教学方式有关.
的前提下认为:“成绩优秀”与教学方式有关.
【解析】
试题分析:根据频率分布直方图中每个矩形的面积即为概率及概率等于频数比样本容量,求出“成绩优秀”和“成绩不优秀”的人数然后即可填表,再利用附的公式求出![]() 的值再与表中的值比较即可得出结论.
的值再与表中的值比较即可得出结论.
试题解析:由频率分布直方图可得,甲班成绩优秀、成绩不优秀的人数分别为12,38,乙班成绩优秀、成绩不优秀的人数分别为4,46.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | 12 | 4 | 16 |
成绩不优秀 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
根据列联表中数据,K2的观测值
k=![]() ≈4.762.
≈4.762.
由于4.762>3.841,所以在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布
 ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产一种产品,质量测试分为:指标不小于
 为一等品;指标不小于
为一等品;指标不小于 且小于
且小于 为二等品;指标小于
为二等品;指标小于 为三等品。其中每件一等品可盈利
为三等品。其中每件一等品可盈利 元,每件二等品可盈利
元,每件二等品可盈利 元,每件三等品亏损
元,每件三等品亏损 元。现对学徒甲和正式工人乙生产的产品各
元。现对学徒甲和正式工人乙生产的产品各 件的检测结果统计如下:
件的检测结果统计如下:测试指标






甲





乙






根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率。求:
(1)乙生产一件产品,盈利不小于
 元的概率;
元的概率;(2)若甲、乙一天生产产品分别为
 件和
件和 件,估计甲、乙两人一天共为企业创收多少元?
件,估计甲、乙两人一天共为企业创收多少元?(3)从甲测试指标为
 与乙测试指标为
与乙测试指标为 共
共 件产品中选取
件产品中选取 件,求两件产品的测试指标差的绝对值大于
件,求两件产品的测试指标差的绝对值大于 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的最小正周期;
的最小正周期;(Ⅱ)求函数
 在区间
在区间 上的最值以及相应的x的取值.
上的最值以及相应的x的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中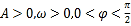 )的图象如图所示:
)的图象如图所示:
(1)求函数
 的解析式及其对称轴的方程;
的解析式及其对称轴的方程;(2)当
 时,方程
时,方程 有两个不等的实根
有两个不等的实根 ,求实数
,求实数 的取值范围,并求此时
的取值范围,并求此时 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…,
 ,…,即当
,…,即当  <n≤
<n≤  (k∈N*)时,
(k∈N*)时, 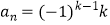 .记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
.记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
(1)求P11中元素个数;
(2)求集合P2000中元素个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
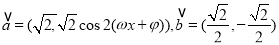 ,其中
,其中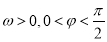 .函数
.函数 的图象过点
的图象过点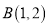 ,点
,点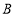 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.(Ⅰ)求函数
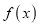 的单调递减区间;
的单调递减区间;(Ⅱ)计算
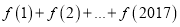 的值;
的值;(Ⅲ)设函数
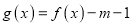 ,试讨论函数
,试讨论函数 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
相关试题

