【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最值以及相应的x的取值.
上的最值以及相应的x的取值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 时,
时,![]() 取得最大值2;
取得最大值2;![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
【解析】
(Ⅰ)利用二倍角和两角和与差以及辅助角公式将函数化为y=Asin(ωx+φ)的形式,利用三角函数的周期公式求函数的最小正周期.
(Ⅱ)利用x∈[![]() ,
,![]() ]上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值.
]上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值.
(Ⅰ)因为函数f(x)=4cosxsin(x![]() )
)![]() 1.
1.
化简可得:f(x)=4cosxsinxcos![]() 4cos2xsin
4cos2xsin![]() 1
1
![]() sin2x+2cos2x
sin2x+2cos2x![]() 1
1![]() sin2x+cos2x=2sin(2x
sin2x+cos2x=2sin(2x![]() )
)
所以![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() .
.
当![]() ,即
,即![]() 时,f(x)取得最大值2;
时,f(x)取得最大值2;
当![]() ,即
,即![]() 时,f(x)取得最小值-1.
时,f(x)取得最小值-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的五个区域中,中心区
 域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
A. 56 B. 72 C. 64 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布
 ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产一种产品,质量测试分为:指标不小于
 为一等品;指标不小于
为一等品;指标不小于 且小于
且小于 为二等品;指标小于
为二等品;指标小于 为三等品。其中每件一等品可盈利
为三等品。其中每件一等品可盈利 元,每件二等品可盈利
元,每件二等品可盈利 元,每件三等品亏损
元,每件三等品亏损 元。现对学徒甲和正式工人乙生产的产品各
元。现对学徒甲和正式工人乙生产的产品各 件的检测结果统计如下:
件的检测结果统计如下:测试指标






甲





乙






根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率。求:
(1)乙生产一件产品,盈利不小于
 元的概率;
元的概率;(2)若甲、乙一天生产产品分别为
 件和
件和 件,估计甲、乙两人一天共为企业创收多少元?
件,估计甲、乙两人一天共为企业创收多少元?(3)从甲测试指标为
 与乙测试指标为
与乙测试指标为 共
共 件产品中选取
件产品中选取 件,求两件产品的测试指标差的绝对值大于
件,求两件产品的测试指标差的绝对值大于 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.

根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
甲班(A方式)
乙班(B方式)
总计
成绩优秀
成绩不优秀
总计
附:K2=
 .
.P(K2≥k)
0.25
0.15
0.10
0.05
0.025
k
1.323
2.072
2.706
3.841
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中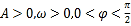 )的图象如图所示:
)的图象如图所示:
(1)求函数
 的解析式及其对称轴的方程;
的解析式及其对称轴的方程;(2)当
 时,方程
时,方程 有两个不等的实根
有两个不等的实根 ,求实数
,求实数 的取值范围,并求此时
的取值范围,并求此时 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…,
 ,…,即当
,…,即当  <n≤
<n≤  (k∈N*)时,
(k∈N*)时, 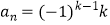 .记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
.记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
(1)求P11中元素个数;
(2)求集合P2000中元素个数.
相关试题

