【题目】某企业生产一种产品,质量测试分为:指标不小于![]() 为一等品;指标不小于
为一等品;指标不小于![]() 且小于
且小于![]() 为二等品;指标小于
为二等品;指标小于![]() 为三等品。其中每件一等品可盈利
为三等品。其中每件一等品可盈利![]() 元,每件二等品可盈利
元,每件二等品可盈利![]() 元,每件三等品亏损
元,每件三等品亏损![]() 元。现对学徒甲和正式工人乙生产的产品各
元。现对学徒甲和正式工人乙生产的产品各![]() 件的检测结果统计如下:
件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率。求:
(1)乙生产一件产品,盈利不小于![]() 元的概率;
元的概率;
(2)若甲、乙一天生产产品分别为![]() 件和
件和![]() 件,估计甲、乙两人一天共为企业创收多少元?
件,估计甲、乙两人一天共为企业创收多少元?
(3)从甲测试指标为![]() 与乙测试指标为
与乙测试指标为![]() 共
共![]() 件产品中选取
件产品中选取![]() 件,求两件产品的测试指标差的绝对值大于
件,求两件产品的测试指标差的绝对值大于![]() 的概率.
的概率.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 元;(3)
元;(3) ![]()
【解析】
(1)设事件![]() 表示“乙生产一件产品,盈利不小于25元”,即该产品的测试指标不小于80,由此能求出乙生产一件产品,盈利不小于25元的概率.
表示“乙生产一件产品,盈利不小于25元”,即该产品的测试指标不小于80,由此能求出乙生产一件产品,盈利不小于25元的概率.
(2)由表格知甲生产的一等品、二等品、三等品比例为即![]() ,所以甲一天生产30件产品,其中一等品有3件,二等品有21件,三等品有6件;由表格知乙生产的一等品、二等品、三等品比例为
,所以甲一天生产30件产品,其中一等品有3件,二等品有21件,三等品有6件;由表格知乙生产的一等品、二等品、三等品比例为![]() ,所以乙一天生产20件产品,其中一等品有6件,二等品有12件,三等品有2件,由此能求出甲、乙两人一天共为企业创收1195元.
,所以乙一天生产20件产品,其中一等品有6件,二等品有12件,三等品有2件,由此能求出甲、乙两人一天共为企业创收1195元.
(3)设甲测试指标为![]() ,
,![]() 的7件产品用
的7件产品用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示,乙测试指标为
表示,乙测试指标为![]() ,
,![]() 的7件产品用
的7件产品用![]() ,
,![]() 表示,利用列举法能求出两件产品的测试指标差的绝对值大于10的概率.
表示,利用列举法能求出两件产品的测试指标差的绝对值大于10的概率.
(1)设事件![]() 表示“乙生产一件产品,盈利不小于
表示“乙生产一件产品,盈利不小于![]() 元”,即该产品的测试指标不小于
元”,即该产品的测试指标不小于![]() ,则
,则![]() ;
;
(2)甲一天生产![]() 件产品,其中一等品有
件产品,其中一等品有![]() 件;二等品有
件;二等品有![]() 件;
件;
三等品有![]() 件;
件;
甲一天生产![]() 件产品,其中一等品有
件产品,其中一等品有![]() 件;二等品有
件;二等品有![]() 件;
件;
三等品有![]()
![]() ,即甲、乙两人一天共为企业创收
,即甲、乙两人一天共为企业创收![]() 元;
元;
(3)设甲测试指标为![]() 的
的![]() 件产品用
件产品用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示,乙测试指标为
表示,乙测试指标为![]() 的
的![]() 件产品用
件产品用![]() ,
,![]() 表示,用
表示,用![]() (
(![]() ,
,![]() 且
且![]() )表示从
)表示从![]() 件产品中选取
件产品中选取![]() 件产品的一个结果.
件产品的一个结果.
不同结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有36个不同结果.
,共有36个不同结果.
设事件![]() 表示“选取的两件产品的测试指标差的绝对值大于
表示“选取的两件产品的测试指标差的绝对值大于![]() ”,即从甲、乙生产的产品中各取
”,即从甲、乙生产的产品中各取![]() 件产品,不同的结果为
件产品,不同的结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 个不同结果.
个不同结果.
则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过
经过 ,
, ,
, 三点.
三点.(1)求圆
 的标准方程;
的标准方程;(2)若过点N
 的直线
的直线 被圆
被圆 截得的弦AB的长为
截得的弦AB的长为 ,求直线
,求直线 的倾斜角.
的倾斜角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的五个区域中,中心区
 域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
A. 56 B. 72 C. 64 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布
 ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的最小正周期;
的最小正周期;(Ⅱ)求函数
 在区间
在区间 上的最值以及相应的x的取值.
上的最值以及相应的x的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.

根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
甲班(A方式)
乙班(B方式)
总计
成绩优秀
成绩不优秀
总计
附:K2=
 .
.P(K2≥k)
0.25
0.15
0.10
0.05
0.025
k
1.323
2.072
2.706
3.841
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中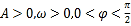 )的图象如图所示:
)的图象如图所示:
(1)求函数
 的解析式及其对称轴的方程;
的解析式及其对称轴的方程;(2)当
 时,方程
时,方程 有两个不等的实根
有两个不等的实根 ,求实数
,求实数 的取值范围,并求此时
的取值范围,并求此时 的值.
的值.
相关试题

