【题目】如图,在平行四边形ABCD中,P,Q分别是BC和CD的中点. 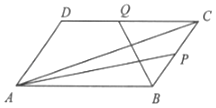
(1)若AB=2,AD=1,∠BAD=60°,求 ![]() 及cos∠BAC的余弦值;
及cos∠BAC的余弦值;
(2)若 ![]() =λ
=λ ![]() +
+ ![]() ,求λ+μ的值.
,求λ+μ的值.
参考答案:
【答案】
(1)解:∵平行四边形ABCD中,AB=2,AD=1,∠BAD=60°,
∴ ![]() =
= ![]() (
( ![]() +
+ ![]() )=
)= ![]() 2+
2+ ![]()
![]() =22+2×1×cos60°=5,
=22+2×1×cos60°=5,
| ![]() |2=
|2= ![]() 2=(
2=( ![]() +
+ ![]() )2=
)2= ![]() 2+2
2+2 ![]()
![]() +
+ ![]() 2=22+2×2×1×cos60°+1=7,
2=22+2×2×1×cos60°+1=7,
∴| ![]() |=
|= ![]() ,
,
cos∠BAC= 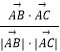 =
= ![]() =
= ![]()
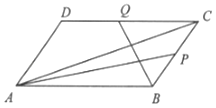
(2)解:∵P,Q分别是BC和CD的中点.
∴ ![]() =
= ![]() +
+ ![]()
![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
∵ ![]() =λ
=λ ![]() +
+ ![]() ,
,
∴ ![]() +
+ ![]() =λ(
=λ( ![]() +
+ ![]()
![]() )+μ(
)+μ( ![]() ﹣
﹣ ![]()
![]() ),
),
∴ 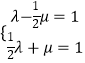 ,
,
解得: ![]() ,
,
∴λ+μ= ![]()
【解析】(1)由已知中AB=2,AD=1,∠BAD=60°,代入向量数量积公式,可得 ![]()
![]() ,求出|
,求出| ![]() |,代入cos∠BAC=
|,代入cos∠BAC= 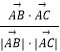 可得cos∠BAC的余弦值;(2)若
可得cos∠BAC的余弦值;(2)若 ![]() =λ
=λ ![]() +
+ ![]() ,则
,则 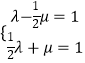 ,解得答案.
,解得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(2x+3)+x2
(1)讨论f(x)的单调性;
(2)求f(x)在区间[﹣ ,
,  ]的最大值和最小值.
]的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
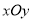 中,已知圆
中,已知圆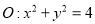 ,椭圆
,椭圆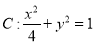 ,
, 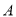 为椭圆
为椭圆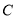 的右顶点,过原点且异于
的右顶点,过原点且异于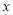 轴的直线与椭圆
轴的直线与椭圆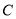 交于
交于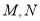 两点,
两点, 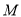 在
在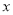 轴的上方,直线
轴的上方,直线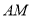 与圆
与圆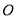 的另一交点为
的另一交点为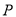 ,直线
,直线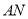 与圆
与圆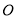 的另一交点为
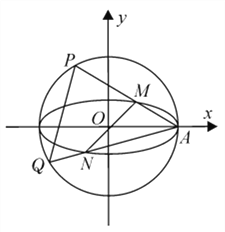
的另一交点为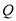 ,
,
(1)若
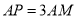 ,求直线
,求直线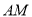 的斜率;
的斜率;(2)设
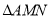 与
与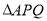 的面积分别为
的面积分别为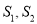 ,求
,求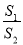 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log
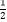 (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费
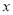 (百万元),可增加销售额约为
(百万元),可增加销售额约为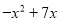 (百万元)(
(百万元)(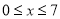 )
)(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费
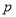 (百万元),可增加销售额约为
(百万元),可增加销售额约为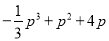 (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益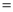 销售额
销售额 成本)
成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
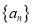 各项均为正数,其前
各项均为正数,其前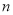 项和为
项和为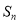 ,且
,且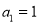 ,
, 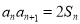 .
.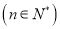
(Ⅰ)求数列
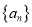 的通项公式;
的通项公式;(Ⅱ)求数列
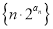 的前
的前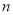 项和
项和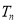 .
.
相关试题

