【题目】如图所示,在![]() 中,
中, ![]() 的中点为
的中点为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .固定边
.固定边![]() ,在平面内移动顶点
,在平面内移动顶点![]() ,使得圆
,使得圆![]() 与边
与边![]() ,边
,边![]() 的延长线相切,并始终与
的延长线相切,并始终与![]() 的延长线相切于点
的延长线相切于点![]() ,记顶点
,记顶点![]() 的轨迹为曲线
的轨迹为曲线![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为坐标原点如图所示建立平面直角坐标系.
为坐标原点如图所示建立平面直角坐标系.
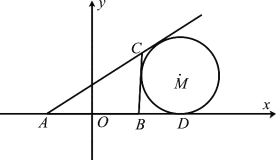
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】【试题分析】(1)依据题设条件运用椭圆的定义进行分析探求;(2)借助题设条件运用直线与椭圆的位置关系进行分析求解:
(Ⅰ)依题意得![]() ,设动圆
,设动圆![]() 与边
与边![]() 的延长线相切于
的延长线相切于![]() ,与边
,与边![]() 相切于
相切于![]() , 则
, 则![]()
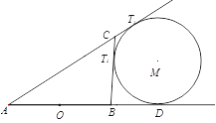
所以![]()
![]() 所以点
所以点![]() 轨迹
轨迹![]() 是以
是以![]() 为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线
为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线![]() 的方程为
的方程为![]() .
.

由于曲线![]() 要挖去长轴两个顶点,所以直线
要挖去长轴两个顶点,所以直线![]() 斜率存在且不为
斜率存在且不为![]() ,所以可设直线
,所以可设直线![]()
由![]() 得
得![]() ,
,![]() ,同理可得:
,同理可得: ![]() ,
,![]() ;
;
所以![]() ,
, ![]()
又![]() ,所以
,所以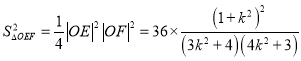 令
令![]() ,
,
则![]() 且
且![]() ,所以
,所以 
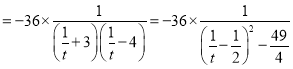 又
又![]() ,所以
,所以![]() ,
,
所以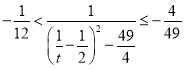 ,
,
所以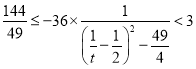 ,所以
,所以![]() ,
,
所以![]() 面积的取值范围为
面积的取值范围为![]() .
.
【法二】
依题意得直线![]() 斜率不为0,且直线
斜率不为0,且直线![]() 不过椭圆的顶点,则可设直线
不过椭圆的顶点,则可设直线![]() :
: ![]() ,且
,且![]() 。
。
设![]() ,又以
,又以![]() 为直径的圆经过点
为直径的圆经过点![]() ,则
,则![]() ,所以
,所以![]()
由![]() 得
得![]() ,则
,则![]()
且![]() ,所以
,所以![]()
又![]()
![]() 代入①得:
代入①得: ![]() ,所以
,所以![]() ,
,
代入②得: ![]() 恒成立所以
恒成立所以![]() 且
且![]() .
.
又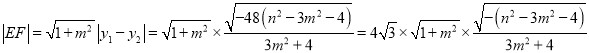 ;
;
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以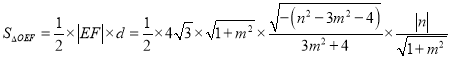
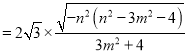
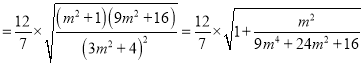
(Ⅰ)当![]() 时,
时, ![]() ;
;
(Ⅱ)当![]() 且
且![]() 时,
时,
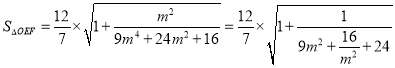 ,
,
又![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”,所以
”,所以![]() ,
,
所以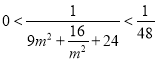 ,所以
,所以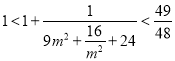 ,
,
所以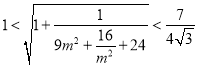 ,所以
,所以![]() ;
;
综合(1),(2)知![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )

A.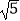
B.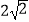
C.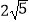
D.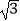
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足log3an+1=log3an+1(n∈N*),且a2+a4+a6=9,则log
 (a5+a7+a9)的值是( )
(a5+a7+a9)的值是( )
A.﹣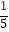
B.﹣5
C.5
D.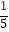
-
科目: 来源: 题型:
查看答案和解析>>【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S=
 .现有周长为2
.现有周长为2  +
+  的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=(  ﹣1):
﹣1):  :(
:(  +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,
时,  恒成立,求
恒成立,求 的取值范围;
的取值范围;(Ⅱ)当
 时,研究函数
时,研究函数 的零点个数;
的零点个数;(Ⅲ)求证:
 (参考数据:
(参考数据:  ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+(a+8)x+a2+a﹣12(a<0),且f(a2﹣4)=f(2a﹣8),则
 的最小值为( )
的最小值为( )
A.
B.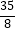
C.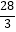
D.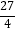
-
科目: 来源: 题型:
查看答案和解析>>【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟)

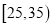
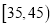


次数
8
14
8
8
2
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为
 分钟.
分钟.(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设
 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求 的分布列和期望.
的分布列和期望.(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
相关试题

