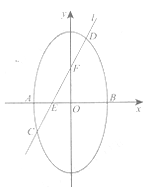
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)联立直线方程与椭圆方程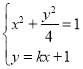 ,消去未知数
,消去未知数![]() 得到关于
得到关于![]() 的方程为:
的方程为:![]() ,
,![]() 显然成立,设
显然成立,设![]() ,于是可以得出
,于是可以得出![]() 和
和![]() ,根据直线
,根据直线![]() 求得
求得![]() ,
,![]() ,于是根据
,于是根据![]() 有:
有:![]() ,就可以求出
,就可以求出![]() 的值;(2)
的值;(2)![]() ,所以
,所以![]() ,则平方有
,则平方有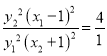 (*),又因为
(*),又因为![]() ,
,![]() ,代入(*)得:
,代入(*)得: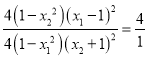 ,于是整理可得:
,于是整理可得:![]() ,整理后得到关于
,整理后得到关于![]() 和
和![]() 的表达式,即得到关于
的表达式,即得到关于![]() 的表达式,于是可以求出
的表达式,于是可以求出![]() 值.
值.
试题解析:(I)设![]()
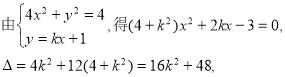
![]()
由已知![]()
又![]()
所以![]()
所以![]() ,
,
符合题意,
所以,所求直线l的方程为![]()
(II)![]() ,
,![]() ,
,
所以![]()
平方得![]()
![]() 代入上式,
代入上式,
计算得![]()
所以![]()
因为![]()
所以k=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知过点
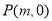 的直线
的直线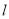 的参数方程是
的参数方程是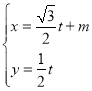 (
(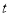 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点,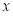 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线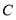 的极坐标方程式为
的极坐标方程式为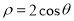 .
.(Ⅰ)求直线
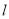 的普通方程和曲线
的普通方程和曲线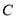 的直角坐标方程;
的直角坐标方程;(Ⅱ)若直线
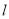 与曲线
与曲线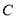 交于两点
交于两点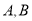 ,且
,且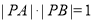 ,求实数
,求实数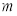 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 的前三项分别为λ,6,3λ,前n项和为Sn,且Sk=165.
的前三项分别为λ,6,3λ,前n项和为Sn,且Sk=165.(1)求λ及k的值;
(2)设bn=
 ,且数列
,且数列 的前n项和Tn,证明:
的前n项和Tn,证明: ≤Tn<1.
≤Tn<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
, ,
, 面
面 ,设
,设 为
为 中点,点
中点,点 在线段
在线段 上,且
上,且 .
.
(1)求证:
 平面
平面 ;
;(2)设异面直线
 与
与 的夹角为
的夹角为 ,若
,若 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
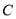 :
: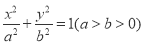 的左右焦点分别为
的左右焦点分别为 ,过
,过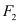 作垂直于
作垂直于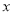 轴的直线
轴的直线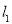 交椭圆
交椭圆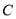 于
于 两点,且满足
两点,且满足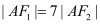 .
.(1)求椭圆
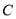 的离心率;
的离心率;(2)过
 作斜率为
作斜率为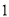 的直线
的直线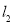 交
交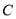 于
于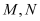 两点.
两点. 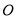 为坐标原点,若
为坐标原点,若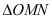 的面积为
的面积为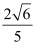 ,求椭圆
,求椭圆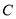 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
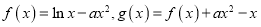 .
.(1)求函数
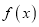 的极值;
的极值;(2)设
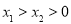 ,比较
,比较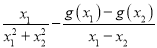 与1的大小关系,并说明理由.
与1的大小关系,并说明理由.
相关试题

