【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,比较
,比较![]() 与1的大小关系,并说明理由.
与1的大小关系,并说明理由.
参考答案:
【答案】(1)当![]() 时,函数
时,函数![]() 无极值,当
无极值,当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,无极小值;(2)
,无极小值;(2)![]() ,理由见解析.
,理由见解析.
【解析】
试题分析:(1)依题意![]() ,分子是一个二次项系数含有参数的式子,所以要对
,分子是一个二次项系数含有参数的式子,所以要对![]() 进行分类讨论,根据开口方向,将
进行分类讨论,根据开口方向,将![]() 分成
分成![]() 和
和![]() 两类来讨论函数的单调区间和极值;(2)
两类来讨论函数的单调区间和极值;(2)![]() ,即比较
,即比较![]() 与
与![]() 的大小. 令
的大小. 令![]() ,即比较
,即比较![]() 与
与![]() 的大小.构造函数
的大小.构造函数![]() 利用导数求得其最大值为
利用导数求得其最大值为![]() ,得证.
,得证.
试题解析:
(1)依题意![]()
①若![]() ,则
,则![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 无极值;
无极值;
②若![]() ,则
,则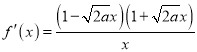 ,此时
,此时![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为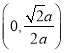 ,单调减区间为
,单调减区间为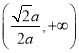 ,
,
故函数![]() 的极大值为
的极大值为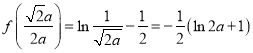 ,无极小值.
,无极小值.
综上所述,当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,无极小值
,无极小值
(2)依题意,![]() ,
,
要比较![]() 与1的大小 ,即比较
与1的大小 ,即比较![]() 与
与![]() 的大小.
的大小.
∵![]() ,∴可比较
,∴可比较![]() 与
与![]() 的大小
的大小
令![]() ,即比较
,即比较![]() 与
与![]() 的大小.
的大小.
设![]() ,
,
则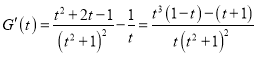 ,
,
因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,所以
,所以![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
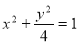 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线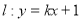 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.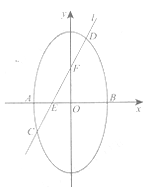
(1)若
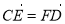 ,求直线
,求直线 的方程;
的方程;(2)设直线AD,CB的斜率分别为
 ,若
,若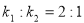 ,求k的值.
,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
, ,
, 面
面 ,设
,设 为
为 中点,点
中点,点 在线段
在线段 上,且
上,且 .
.
(1)求证:
 平面
平面 ;
;(2)设异面直线
 与
与 的夹角为
的夹角为 ,若
,若 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
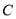 :
: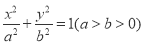 的左右焦点分别为
的左右焦点分别为 ,过
,过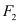 作垂直于
作垂直于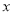 轴的直线
轴的直线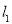 交椭圆
交椭圆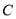 于
于 两点,且满足
两点,且满足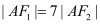 .
.(1)求椭圆
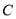 的离心率;
的离心率;(2)过
 作斜率为
作斜率为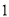 的直线
的直线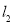 交
交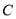 于
于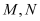 两点.
两点. 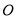 为坐标原点,若
为坐标原点,若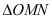 的面积为
的面积为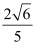 ,求椭圆
,求椭圆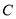 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列{an}的公比为q,其前n项的积为Tn,并且满足条件a1>1,a49a50-1>0,(a49-1)(a50-1)<0.给出下列结论:
①0<q<1;②a1a99-1<0;③T49的值是Tn中最大的;④使Tn>1成立的最大自然数n等于98.
其中所有正确结论的序号是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为
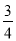 ,乙每关通过的概率为
,乙每关通过的概率为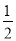 ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.(1)求甲、乙获得2000元奖金的概率;
(2)设
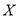 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量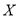 的分布列和数学期望
的分布列和数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(
 )班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.
)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.

(1)求全班人数及分数在
 之间的频数,并估计该班的平均分数;
之间的频数,并估计该班的平均分数;(2)若要从分数在
 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在 之间的概率.
之间的概率.
相关试题

