【题目】已知抛物线![]() 的顶点为原点
的顶点为原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点, ![]() 在第一象限,
在第一象限, ![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据圆的圆心为抛物线的焦点,可求得![]() ,即可求得抛物线方程
,即可求得抛物线方程![]() ;(2)若是等差中项,那么
;(2)若是等差中项,那么![]() ,那么
,那么![]() ,再根据抛物线的焦点弦长可知
,再根据抛物线的焦点弦长可知![]() ,将问题转化为根与系数的关系,求出直线方程.
,将问题转化为根与系数的关系,求出直线方程.
试题解析:(1)根据已知设抛物线![]() 的方程为
的方程为![]() .
.
∵圆![]() 的方程为
的方程为![]() ,
,
∴圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() .
.
∴![]() ,解得
,解得![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)∵![]() 是
是![]() 与
与![]() 的等差中项,∴
的等差中项,∴![]() .
.
∴![]() .
.
若![]() 垂直于
垂直于![]() 轴,则
轴,则![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() .
.
此时![]() ,即直线
,即直线![]() 不满足题意.
不满足题意.
若![]() 不垂直于
不垂直于![]() 轴,设
轴,设![]() 的斜率为
的斜率为![]() ,由已知得
,由已知得![]() ,
, ![]() 的方程为
的方程为![]() .
.
设![]() ,由
,由![]() 得
得![]() .
.
∴![]() .
.
∵抛物线![]() 的准线为
的准线为![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() 化为
化为![]() ,
,
∵![]() ,∴
,∴![]() 有两个不相等实数根.
有两个不相等实数根.
∴![]() 满足题意,即直线
满足题意,即直线![]() 满足题意.
满足题意.
∴存在满足要求的直线![]() ,它的方程为
,它的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =f(2x)
=f(2x)
(1)用定义证明函数g(x)在(﹣∞,0)上为减函数.
(2)求g(x)在(﹣∞,﹣1]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+2x+b>0(a≠0)的解集为
 ,且a>b,则
,且a>b,则  的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
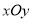 中,直线
中,直线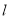 的参数方程为
的参数方程为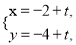 (
(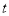 为参数).以原点
为参数).以原点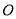 为极点,
为极点, 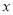 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线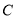 的极坐标方程为
的极坐标方程为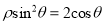 .直线
.直线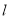 交曲线
交曲线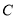 于
于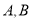 两点.
两点.(1)写出直线
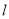 的极坐标方程和曲线
的极坐标方程和曲线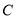 的直角坐标方程;
的直角坐标方程;(2)设点
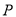 的直角坐标为
的直角坐标为 ,求点
,求点 到
到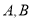 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ,求使得不等式
,求使得不等式  恒成立的实数k的取值范围.
恒成立的实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是自然对数的底数,
是自然对数的底数,  ,
,  ,
,  ,
,  .
.(1)设
 ,求
,求 的极值;
的极值;(2)设
 ,求证:函数
,求证:函数 没有零点;
没有零点;(3)若
 ,设
,设 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱柱
 中,点
中,点 分别为
分别为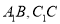 的中点.
的中点.
(1)求证:
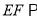 平面
平面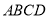 ;
;(2)若四棱柱
 是长方体,且
是长方体,且 ,求平面
,求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
相关试题

