【题目】已知函数![]() ,其中
,其中![]() ,且
,且![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若
,若![]() 存在极大值,且对于
存在极大值,且对于![]() 的一切可能取值,
的一切可能取值, ![]() 的极大值均小于
的极大值均小于![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)计算出导数![]() ,由不等式
,由不等式![]() 得增区间,由
得增区间,由![]() 得减区间,注意要按
得减区间,注意要按![]() 的正负分类讨论,
的正负分类讨论, ![]() 的正负对定义域有影响;
的正负对定义域有影响;
(2)求出导数![]() ,因此必须有
,因此必须有![]() ,
, ![]() 才能有两个不等实根,
才能有两个不等实根, ![]() 的两实根为
的两实根为![]() ,
, ![]() ,极大值为
,极大值为![]() ,由求根公式得
,由求根公式得![]() ,令
,令![]() (作为
(作为![]() 的函数),同理由导数知识得
的函数),同理由导数知识得![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() ,由
,由![]() 可得
可得![]() 的范围.
的范围.
试题解析:
(1) ![]() 时,
时, ![]() ,故
,故![]()
当![]() 时,
时, ![]() ,由
,由![]() ,得
,得![]() 得
得![]()
因此![]() 的单调递增区间为:
的单调递增区间为: ![]() ,单调递减区间为:
,单调递减区间为: ![]()
当![]() 时,
时, ![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]()
因此单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(2)由题![]() ,显然
,显然![]() ,设
,设![]() 的两根为
的两根为![]() ,则当
,则当![]() 或
或![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,故
,故![]() 极大
极大![]() 只可能是
只可能是![]() ,且
,且![]() ,知
,知![]() ,又
,又![]() ,故
,故![]() ,且
,且![]() ,
,
从而![]() 令
令![]() ,
,
则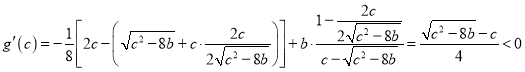 ,
,
故![]() 在
在![]() 单减,从而
单减,从而![]() ,
,
因此![]() ,解得
,解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
, 
 ,
,  平面
平面 ,
,  .设
.设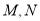 分别为
分别为 的中点.
的中点.
(1)求证:平面
 ∥平面
∥平面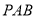 ;
;(2)求二面角
 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
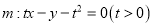 与椭圆
与椭圆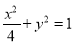 交于
交于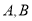 两点,与
两点,与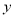 轴交于
轴交于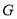 点,
点, 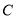 为弦
为弦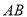 的中点,直线
的中点,直线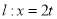 分别与直线
分别与直线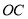 和直线
和直线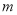 交于
交于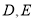 两点.
两点.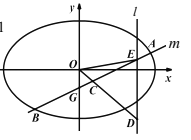
(1)求直线
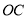 的斜率和直线
的斜率和直线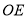 的斜率之积;
的斜率之积;(2)分别记
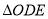 和
和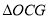 的面积为
的面积为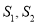 ,是否存在正数
,是否存在正数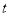 ,使得
,使得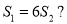 若存在,求出
若存在,求出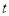 的取值;若不存在,说明理由.
的取值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知D,E,F分别为△ABC的边BC,CA,AB的中点,记
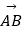 =a ,
=a , 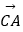 =b.则下列命题中正确的个数是( )
=b.则下列命题中正确的个数是( )
①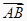 =
= 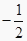 a-b;②
a-b;② 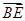 =a+
=a+ 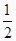 b;③
b;③ 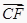 =
= 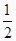 a+
a+ 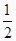 b;④
b;④ 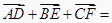 0.
0.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G.

(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为
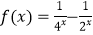 .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值.
相关试题

