【题目】已知D,E,F分别为△ABC的边BC,CA,AB的中点,记 ![]() =a ,
=a , ![]() =b.则下列命题中正确的个数是( )
=b.则下列命题中正确的个数是( )
① ![]() =
= ![]() a-b;②
a-b;② ![]() =a+
=a+ ![]() b;③
b;③ ![]() =
= ![]() a+
a+ ![]() b;④
b;④ ![]() 0.
0.
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解答:因为 ![]() -b-a,故①错误;因为
-b-a,故①错误;因为 ![]() =a+
=a+ ![]() b,故②为正确;因为
b,故②为正确;因为 ![]() b+
b+ ![]() (-b-a)=
(-b-a)= ![]() (a+b),故③为正确;
(a+b),故③为正确;
因为 ![]() 0,故④正确,选C.
0,故④正确,选C.
分析:本题主要考查了向量的三角形法则、向量加减混合运算及其几何意义,解决问题的关键是根据所给向量满足条件结合题设条件进行发现判断即可.
【考点精析】解答此题的关键在于理解向量的三角形法则的相关知识,掌握三角形加法法则的特点:首尾相连;三角形减法法则的特点:共起点,连终点,方向指向被减向量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列结论:
①y=x2+1,x∈[﹣1,2],y的值域[2,5]是;
②幂函数图象一定不过第四象限;
③函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
④若loga >1,则a的取值范围是(
>1,则a的取值范围是(  ,1);
,1);
⑤函数f(x)=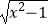 +
+ 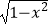 是既奇又偶的函数;
是既奇又偶的函数;
其中正确的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
, 
 ,
,  平面
平面 ,
,  .设
.设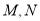 分别为
分别为 的中点.
的中点.
(1)求证:平面
 ∥平面
∥平面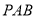 ;
;(2)求二面角
 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
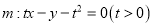 与椭圆
与椭圆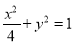 交于
交于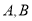 两点,与
两点,与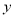 轴交于
轴交于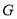 点,
点, 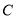 为弦
为弦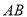 的中点,直线
的中点,直线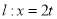 分别与直线
分别与直线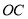 和直线
和直线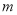 交于
交于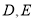 两点.
两点.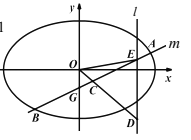
(1)求直线
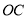 的斜率和直线
的斜率和直线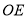 的斜率之积;
的斜率之积;(2)分别记
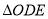 和
和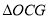 的面积为
的面积为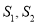 ,是否存在正数
,是否存在正数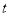 ,使得
,使得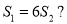 若存在,求出
若存在,求出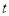 的取值;若不存在,说明理由.
的取值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 ,且
,且
(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)设
 ,若
,若 存在极大值,且对于
存在极大值,且对于 的一切可能取值,
的一切可能取值,  的极大值均小于
的极大值均小于 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G.

(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
相关试题

