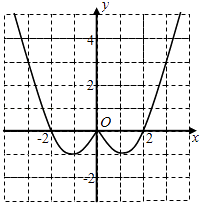
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
参考答案:
【答案】
(1)解:因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如有图:
所以f(x)的递增区间是(﹣1,0),(1,+∞)
(2)解:设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以x>0时,f(x)=x2﹣2x,
故f(x)的解析式为 ![]()
值域为{y|y≥﹣1}
【解析】(1)因为函数为偶函数,故图象关于y轴对称,由此补出完整函数f(x)的图象即可,再由图象直接可写出f(x)的增区间.(2)可由图象利用待定系数法求出x>0时的解析式,也可利用偶函数求解析式,值域可从图形直接观察得到.
【考点精析】关于本题考查的函数的值域和函数的单调性,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知D,E,F分别为△ABC的边BC,CA,AB的中点,记
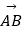 =a ,
=a , 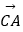 =b.则下列命题中正确的个数是( )
=b.则下列命题中正确的个数是( )
①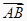 =
= 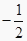 a-b;②
a-b;② 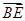 =a+
=a+ 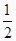 b;③
b;③ 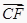 =
= 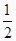 a+
a+ 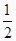 b;④
b;④ 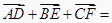 0.
0.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 ,且
,且
(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)设
 ,若
,若 存在极大值,且对于
存在极大值,且对于 的一切可能取值,
的一切可能取值,  的极大值均小于
的极大值均小于 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G.

(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为
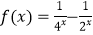 .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价定为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.
(1)设一次订购量为x张,课桌的实际出厂单价为P元,求P关于x的函数关系式P(x);
(2)当一次订购量x为多少时,该家具厂这次销售课桌所获得的利润f(x)最大?其最大利润是多少元?(家具厂售出一张课桌的利润=实际出厂单价﹣成本). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ 或x>﹣
或x>﹣  }
}
C.{x|﹣ <x<﹣
<x<﹣  }
}
D.{x|﹣3<x<﹣2}
相关试题

